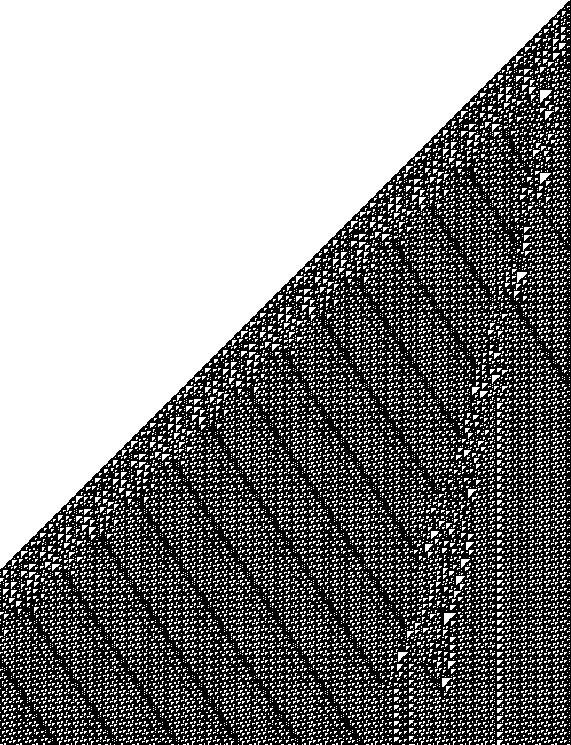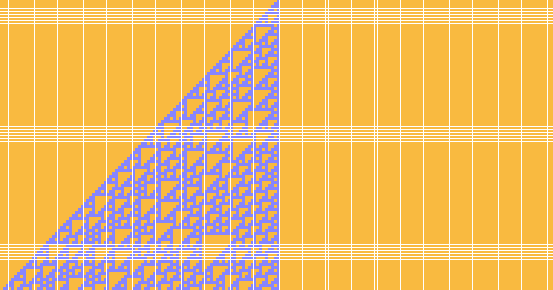
Conclusions

Figure 5.1: One of the reasons that large triangles do not occur often in evolutions is that they do not pack well. Extremely large triangles belong to the Garden of Eden.

Figure 5.2: After the first few hundred generations, a boundary layer stabilizes along the advancing edge of the expansion of a single cell into the vacuum. It still has to come to terms with the right edge. (Figure courtesy Genaro Juarez Martinez)

Figure 5.3: Eventually the expansion of a single cell into the vacuum comes into equilibrium, with A gliders from the left meeting C3's on the right in a reaction which displac es them slightly to the left. (Figure courtesy Genaro Juarez Martinez)

Using cyclic configurations to find gliders has limitations, especially when the gliders are sought against a textured background, as in the case of Rule 110. The idea of the straightjacket consists in fixing the boundary cells of an interval and looking at the evolution so constrained, which is certainly not a new idea by any means. In the case of gliders, the boundary can be staggered according to the velocity of the glider.

However, there is a complication, namely that the postulated boundary may not be compatible with the evolution of the full field, after all. The result is that running out the constrained basin diagram gives a necessary, but not sufficient, condition that the nuclear (transient-free) diagram defines gliders which can be inserted into the given background. Between necessity and sufficiency lies a compatibility problem, expressible via the Post Correspondence Principle, a/k/a the word problem, with a good liklihood of being undecidable: ``It is undecidable whether there exists a glider of arbitrary velocity s/d (displacement/generation) in a textured automaton.''

``Textured'' rules out arbitrary Class III automata unless agreement on an ``ether'' can be reached, whereas Class I and II automata do not have enough texture to raise the word problem out of triviality. In other words, it all depends on whether the sequence the straightjacket program generates is complex enough to create a word problem when checked against the boundary sequence.

Note a difference between the basin calculation and what is proposed here: Basin programs generate trees rooted on loops (and hence loop nuclei) because of the functional character of cyclic evolution. A stipulated boundary has to compensate the degradation of the automaton's interval due to the discrepancy between neighborhood and cell; when there is shifting, it has to be thicker still. Therefore the map of a glider's- width-interval always depends on some boundary cells, but still more at shift points. An interval will always have a successor, but possibly more than one, in contradistinction to the cyclic case; therefore nuclei need not be simple loops. Otherwise there would be no word problem.

As far as actually testing this, the gliders reported by Cook and Lind together with the margins they require imply a greater computational effort than that to which I have been accustomed.