transpose

If a bilinear form is altered by first mapping its left argument, the result is another bilinear form because of the linearity of matrix multiplication. To use a transient notation, suppose that 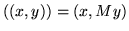$((x, y)) = (x, M y)$. Because

$$((x, a y + b z)) =(x, M ( a y + b z )) = (x, a M y + b M z) = a ((x, y)) + b ((x, y)),$$

the assertion is verified. But inner products are represented by projections from the reciprocal basis, or alternatively, vectors in the dual space, so this new function must be one of them, which prompts calling it the transposed function. Thus, by definition, 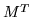$M^T$ is the mapping of the dual space for which

$$\begin{eqnarray*} (M^T x, y) = (x, M y). \end{eqnarray*}$$

Because of the conventional representation of vectors as columns, and functions of the dual space as rows acting on the vectors by inner product, the use of the word transpose merely attests to the tradition of flipping rows to get columns and vice versa. In the fortunate circumstance that 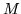$M$ is a square matrix and 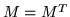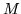$M = M^T$, $M$ is called symmetric. The Gram matrix fulfills this requirement, as did the matrix representation of a symmetric bilinear function. Another possibility is 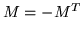$M = - M^T$, making 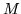$M$ antisymmetric.