index raising and lowering

It is an interesting question, how to turn a matrix into its transpose, just using matrix operations. The simplest thing would be to write

$$\begin{eqnarray*} M^T & = & (M^T M^{-1}) M, \end{eqnarray*}$$

which is not an especially symmetric relationship, and of course supposes that 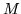$M$ is invertible. Supposing further moment that 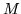$M$, as well as 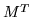$M^T$ had both square roots and inverses, we could have

$$\begin{eqnarray*} M^T & = & (\surd(M)\surd((M^T)^{-1}))^{-1} M \surd(M^{-1})\surd(M^T) \end{eqnarray*}$$

if we wanted it. At least 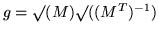$g = \surd(M)\surd((M^T)^{-1})$ is ready for use at any time for writing $M^T = g^{-1}Mg$.