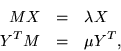
Turning to the consequences of symmetry, in the technical sense of a symmetric matrix, the usual analysis observes that for left and right eigenvectors (writing vectors as columns means that rows are transposes of columns)
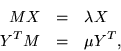
This result holds for any matrix ![]() , symmetric or not, and can be summarized by saying that if we make up two matrices, one a column of left eigenrows and the other a row of right eigencolumns, the two matrices are inverses. Or at least partial inverses, because we still don't know how many eigenvectors there actually are, and maybe there are not enough to complete a basis.
, symmetric or not, and can be summarized by saying that if we make up two matrices, one a column of left eigenrows and the other a row of right eigencolumns, the two matrices are inverses. Or at least partial inverses, because we still don't know how many eigenvectors there actually are, and maybe there are not enough to complete a basis.
If ![]() is itself a symmetric matrix, simply transposing the defining equation
is itself a symmetric matrix, simply transposing the defining equation
![]() to get
to get
![]() shows that eigencolumns are eigenrows, keeping the same eigenvalue. Supposing there were enough eigenvectors to make a basis,
shows that eigencolumns are eigenrows, keeping the same eigenvalue. Supposing there were enough eigenvectors to make a basis, ![]() , a matrix of eigenvectors, would satisfy
, a matrix of eigenvectors, would satisfy ![]() , a condition expressed by saying that
, a condition expressed by saying that ![]() is orthogonalorthogonal matrix.
is orthogonalorthogonal matrix.