The invertibility of the matrix
![]() merits further discussion.
This particular inverse,
merits further discussion.
This particular inverse,
![]() , has a special name -- the resolventresolvent of
, has a special name -- the resolventresolvent of ![]() . But first things first: recalling the axiomatic definition of a determinant, calling the columns of
. But first things first: recalling the axiomatic definition of a determinant, calling the columns of ![]()
![]() , and the coordinate vectors
, and the coordinate vectors ![]() , we have
, we have
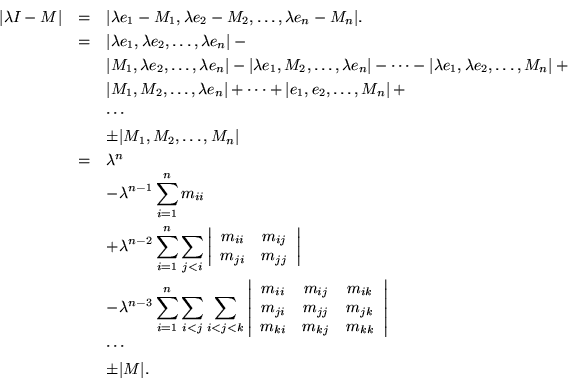
This result exhibits ![]() in terms of its coefficients, which are sums of diagonal minors, with orders corresponding to the power of
in terms of its coefficients, which are sums of diagonal minors, with orders corresponding to the power of ![]() which they multiply. They could be read out directly from the matrix, albeit while performing a greater or lesser quantity of arithmetic to get all the cofactors.
which they multiply. They could be read out directly from the matrix, albeit while performing a greater or lesser quantity of arithmetic to get all the cofactors.
Noteworthy is the role of the negative of the tracetrace (which is the sum of the diagonal elements) as the coefficient of the penultimate power of ![]() , and the determinant in the role of the constant term. If
, and the determinant in the role of the constant term. If ![]() vanishes,
vanishes, ![]() is a root of
is a root of ![]() , and there is a vector for which
, and there is a vector for which ![]() . Of course that prevents
. Of course that prevents ![]() from being invertible; an issue distinct from whether
from being invertible; an issue distinct from whether
![]() vanishes.
vanishes.