resolvent

Continuing on, it turns out that the resolvent can be calculated, in terms of the coefficients of the characteristic polynomial. Needing the adjugate of $(\lambda I - M)$, we start by knowing that it is a polynomial of degree $n-1$ in $\lambda$ because that is the maximum dimension of the cofactors and thus the maximum number of $\lambda$s which could ever be multiplied together. Grouping the coefficients of $\lambda^i$ together in a matrix called $A_i$, set

$$\begin{eqnarray*} (\lambda I - M)^A & = & \sum_{i=0}^{n-1} \lambda^i A_i, \end{eqnarray*}$$

with a corresponding expansion of the characteristic polynomial

$$\begin{eqnarray*} \chi(\lambda) & = & \sum_{i=0}^n c_i\lambda^i. \end{eqnarray*}$$

Then the equation

$$\begin{eqnarray*} (\lambda I - M)(\lambda I - M)^A & = & \chi(\lambda) I \end{eqnarray*}$$

could be subjected to a series of transformations

$$\begin{eqnarray*} (\lambda I - M)\sum_{i=0}^{n-1} \lambda^i A_i & = & \sum_{i... ... \sum_{i=0}^n \{ A_{i-1} - M A_i - c_i I \} \lambda^i & = & O. \end{eqnarray*}$$

to get a result in which the matrix coefficient of each power of $\lambda$ would have to vanish. That produces a chain of substitutions consisting of $A_{i-1} = M A_i + c_i I$ (the missing $A_{-1}$, as well as the nonexistent $A_n$ would both have to be $O$).

$$\begin{eqnarray*} A_{n-1} & = & c_n I \\ A_{n-2} & = & c_n M + c_{n-1} I \\ ... ...A_{-1} & = & c_n M^n + c_{n-1} M^{n-1} + \cdots + c_1 M + c_0 I \end{eqnarray*}$$

Note that these equations are readily summarized in a single matrix equation,

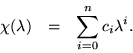
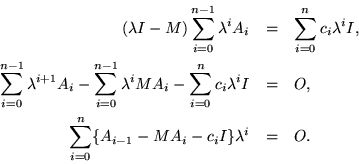
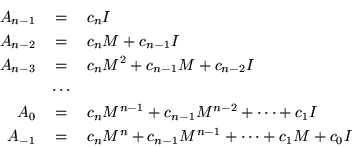
$$\begin{eqnarray*} \left[ \begin{array}{c} O \\ A_0 \\ \ldots \\ A_{n-3} \\ A_... ...\ M \\ \ldots \\ M^{n-2} \\ M^{n-1} \\ M^n \end{array} \right]. \end{eqnarray*}$$

Matrices of the strip antidiagonal form evident in this equation are called Hankel matricesHankel matrix; they occur frequently in such contexts as the moment problem or in fitting least squares approximations.