stable subspaces

Constructing interpolation polynomials based on the characteristic equation leads to a family of orthogonal idempotents resolving the identity. In the confluent case, there are supplementary nilpotent matrices which take up the slack left by the redundant eigenvectors. Since an idempotent satisfies the equation $J^2 = J$ its eigenvalues can only be $0$ or $1$; similarly $0$, can be the only eigenvalue of a matrix which satisfies $N^p = O$. That is the way to get a concise derivation of Sylvester's formula, without going through the steps of constructing a basis, which is the frame of reference likely to be required in applications.

Let $M$ map a vector $X$ to $MX$, which may or may not be parallel to $X$, depending on fortune. If it is not, map this new vector into $M M X$, and so on. Eventually the result has to be dependent on the foregoing vectors, because of the of the dimensionality.

The coefficients of the dependence can be transferred to the matrix powers (supposing, formaly, that a zero power is the unit matrix), resulting in a polynomial in $M$:

$$\begin{eqnarray*} \sum( a_i M_i ) X & = & \varphi(M) X = 0 \end{eqnarray*}$$

which annihilates $X$, although the precise coefficients could possibly differ according to the starting vector. To counter that alternative, note that $M$ commutes with $\varphi(M)$ so that there is a series of vanishing vectors,

$$\begin{eqnarray*} \varphi(M) X & = & 0, \\ \varphi(M) M X & = & 0, \\ \varphi(M) M^2 X & = & 0, \\ \ldots & & \ldots \end{eqnarray*}$$

If they form a basis, then $\varphi(M)$ can only annihilate all of them if it is zero, which is again the Cayley-Hamilton theorem. But the process is fairly haphazard -- what if the original choice was already an eigenvector (consider using the unit matrix)? Or a member of some other stable subspace of less than the full dimension of the space?

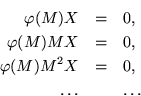
Rather than trusting to luck, it would be possible to start with a basis consisting of vectors $U_i$ comprising the columns of a matrix $U$ to obtain a sequence of polynomials for which $\varphi_i(M)U_i = O$. Not knowing whether they have common factors, it would be necessary to say that

$$\begin{eqnarray*} \prod_{i=1}^n\varphi_i(M)U & = & O \end{eqnarray*}$$

because there would be a factor in the product for every column which would annihilate it. The overall polynomial could possibly have degree $n^2$, the dimension of the space of matrices rather than the space of the vectors. Since we already know from the Cayley-Hamilton theorem that the characteristic polynomial with degree $n$ does the job, there must be many common factors amongst the $\varphi_i$'s.

Just as in the case of repeated roots of the determinantal equation, there are messy cases to be accounted for when a polynomial of lesser degree suffices, or none of the starting vectors leads up to a full basis; as an extreme example, consider finding eigenvectors for the zero matrix or the unit matrix.

If the coefficient of $I$ in $\varphi(M)$ is not zero, implying that the vector chosen for the power search was a good choice, we could set $I$ aside, assume its coefficient to be 1, and take $M$ out of the remaining polynomial as a factor, to get

$$\begin{eqnarray*} inv(M) M & = & I. \end{eqnarray*}$$

In other words, the inverse of a matrix could be calculated using the first few positive powers of the matrix.

This construction of the characteristic polynomial leaves the impression that the set of powers of a matrix is a vector space of the same dimension (or less) as the space on which the matrix itsef operates. Of course the set of all linear mappings from a vector space to itself is another vector space, whose dimension would have to be the square of the original dimension. Polynomials in a single matrix constitute a subspace of Linear(V, V); one might speculate whether there could be be another matrix, generating a second polynomial subspace, such that the entire set of linear mappings were expressible as polynomials in just those two variables.