


Next: stable subspaces
Up: Canonical forms
Previous: Lagrange interpolation polynomials
Contents
Lest it seem that all these results are too good to be true, be assured of that; this form of Lagrange interpolation assumes that all points - that is, eigenvalues - are distinct. In the contrary case, confluent forms of the polynomials may be required; and even then, considerable discretion is required.
When there are multiple roots, they should be grouped together in factoring the characteristic polynomial. Suppose that 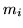 is the multiplicity of
is the multiplicity of 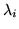 and that there are
and that there are 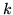 distinct roots:
distinct roots:
This time the Gee's should be defined by
They should be accompanied by the additional polynomials
The factorial and reduced power attest their confluent origin, because these interpolating polynomials are specified by their values and 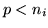 derivatives at each interpolation point
derivatives at each interpolation point 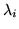 . Note that
. Note that 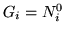 ,
and also that the superscript
,
and also that the superscript 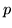 in
in 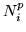 is not quite an exponent, although it behaves like one.
is not quite an exponent, although it behaves like one.
Complications arise for the multiplication table for the 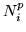 although it is still true that
although it is still true that
Consequently the 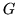 's are still orthogonal idempotents, but they might not quite resolve the unit matrix. In principle, the remainder of the multiplication table could be worked out by calculating and evaluating the derivatives of the products to get the data required for the confluent interpolation.
's are still orthogonal idempotents, but they might not quite resolve the unit matrix. In principle, the remainder of the multiplication table could be worked out by calculating and evaluating the derivatives of the products to get the data required for the confluent interpolation.
Nevertheless their sum,
by failing to vanish at any of the interpolation points, has no zeroes in common with any of the 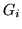 , nor with the characteristic polynomial
, nor with the characteristic polynomial 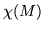 .
That means that the greatest common denominator of G(m) and
.
That means that the greatest common denominator of G(m) and 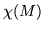 is the constant
is the constant 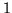 , thanks to which the Euclidean algorithmEuclidean algorithm assures the existence of polynomials
, thanks to which the Euclidean algorithmEuclidean algorithm assures the existence of polynomials
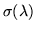 and
and 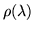 for which
for which
Recognizing that 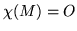 because of the Cayley-Hamilton theorem, the matrix version of the equation requires
because of the Cayley-Hamilton theorem, the matrix version of the equation requires 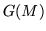 to be invertible given that
to be invertible given that
In order to get the confluent version of Sylvester's formula, consider a Taylor's series for the function 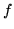 , but written in the more complicated form
, but written in the more complicated form
it has the immediate matrix counterpart
where
are respectively the head, and the tail with a common factor removed, of the Taylor's series based on each eigenvalue. This splitting foresees applying the sum of the Gees, combined with its inverse in the form of the unit matrix, to 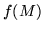 .
.
An inconvenient aspect of this formula is the presence of the factor 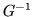 , which compensates for the simple form of the basis polynomials
, which compensates for the simple form of the basis polynomials 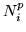 . Alternativley, a resolution of the identity could be used which would avoid having to find and use the overall factor
. Alternativley, a resolution of the identity could be used which would avoid having to find and use the overall factor 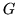 . Consider the identity
. Consider the identity
in which the quotient
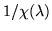 is first resolved into partial fractions, and then multiplied by the numerator
is first resolved into partial fractions, and then multiplied by the numerator 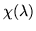 to get a sum of terms similar to the
to get a sum of terms similar to the 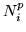 . The difference between the formulations lies in relations between the basis polynomials and their dual basis. In one case, the use of powers complicates the dual, while in the other the dual is formed elegantly by just values and derivatives, but the basis no longer consists of simple power products.
. The difference between the formulations lies in relations between the basis polynomials and their dual basis. In one case, the use of powers complicates the dual, while in the other the dual is formed elegantly by just values and derivatives, but the basis no longer consists of simple power products.



Next: stable subspaces
Up: Canonical forms
Previous: Lagrange interpolation polynomials
Contents
Pedro Hernandez
2004-02-28
![]() is the multiplicity of
is the multiplicity of ![]() and that there are
and that there are ![]() distinct roots:
distinct roots:
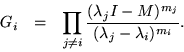
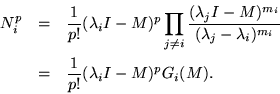
![]() although it is still true that
although it is still true that
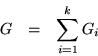
![]() because of the Cayley-Hamilton theorem, the matrix version of the equation requires
because of the Cayley-Hamilton theorem, the matrix version of the equation requires ![]() to be invertible given that
to be invertible given that
![]() , but written in the more complicated form
, but written in the more complicated form
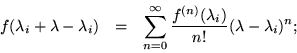
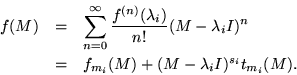
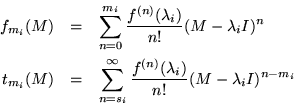
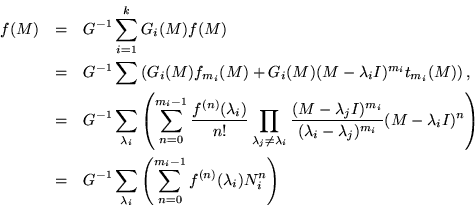
![]() , which compensates for the simple form of the basis polynomials
, which compensates for the simple form of the basis polynomials ![]() . Alternativley, a resolution of the identity could be used which would avoid having to find and use the overall factor
. Alternativley, a resolution of the identity could be used which would avoid having to find and use the overall factor ![]() . Consider the identity
. Consider the identity