null vectors

There are null vectors in the Minkowski metric, which is to say, nonzero vectors with zero norm. What would a null vector look like? Consider $\surd 2 {\bf i}+ {\bf j}+ {\bf k}$.

$$\left[ \begin{array}{cc} 1 & 1+\surd 2 \\ 1 - \surd 2 & - 1, \end{array} \right]$$

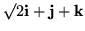whose trace and determinant are both zero, yet it is not the zero matrix. It has to have the Jordan normal form with eigenvalue zero. Those are generally the null vectors; by satisfying 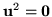${\bf u}^2 = {\bf0}$, they are their own eigenvectors, and manifestly nilpotent.