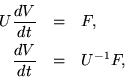solving inhomogeneous equations

First, consider a system inhomogeneous equations written in matrix form:

$$\begin{eqnarray*} \frac{dZ}{dt} & = & R Z + F \end{eqnarray*}$$

Z could be a vector, but all the linearly independent solutions of the system can be treated simultaneously by gathering them up into a matrix as columns. In that case the forcing terms F should be spread out into a matrix as well.

Now suppose that 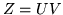$Z = U V$ and recall the rule for differentiating a product:

$$\begin{eqnarray*} \frac{dUV}{dt} & = & \frac{dU}{dt} V + U \frac{dV}{dt}, \end{eqnarray*}$$

whereupon

$$\begin{eqnarray*} \frac{dU}{dt} V + U \frac{dV}{dt} & = & R U V + F. \end{eqnarray*}$$

If the homogeneous equation

$$\begin{eqnarray*} \frac{dU}{dt} & = & R U, \end{eqnarray*}$$

has already been solved, especially from the unit matrix as an initial condition, its terms would drop out of the equation, leaving

$$\begin{eqnarray*} U \frac{dV}{dt} & = & F, \\ \frac{dV}{dt} & = & U^{-1}F, \end{eqnarray*}$$

At this stage, the right hand side of the equation is a completely known matrix of functions, characterizing the solution as a quadrature:

$$\begin{eqnarray*} V(t) & = & V(0) + \int_0^t{U^{-1}(\sigma) F(\sigma) d\sigma}, \end{eqnarray*}$$

and the entire solution by:

$$\begin{eqnarray*} Z(t) & = & U(t)Z(0) + \int_0^t{U(t) U^{-1}(\sigma) F(\sigma) d\sigma}, \end{eqnarray*}$$