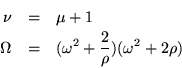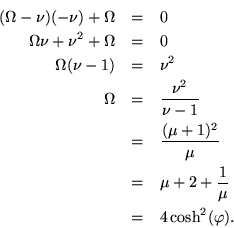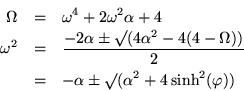Next: Tapered string
Up: A Variety of String
Previous: Point defect
Contents
In a diatomic chain, two different kinds of particles are supposed, but they alternate with one another rather than having similar particles grouped together in sequence. The effect remains the interaction of one group with the other, but now that they are interspersed, the consideration has to be the even numbered particles competing with the odd numbered particles.
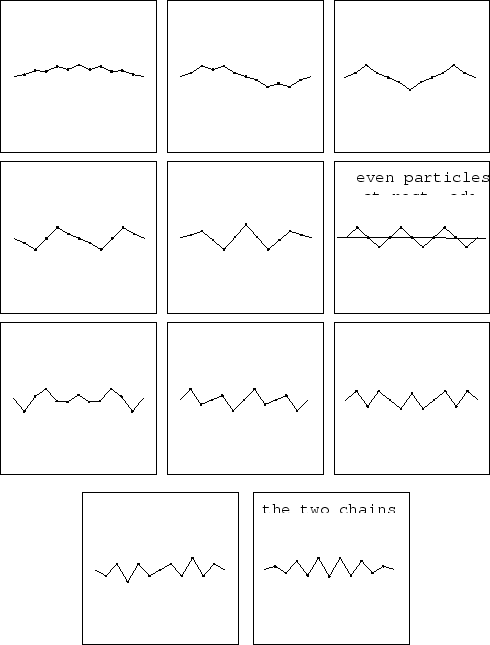
Figure:
heavy and light particles alternate
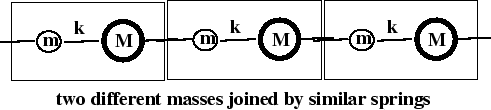 |
The dynamical matrix would look like:
Introducing a mass ratio
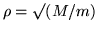 and writing the common factor
and writing the common factor 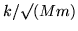 outside the matrix gives the dynamical matrix a better appearance:
outside the matrix gives the dynamical matrix a better appearance:
Mathematically, what could be done is to combine a consecutive pair into a single unit cell by multiplying their wave matrices, and then raising this product to a power. Depending on whether the chain is of even or odd length overall, a single wave matrix may have to be incorporated to finish off the full chain. Although the dispersion relation for a single cell has to be more complicated, the advantage of constant wave numbers irrespective of the number of unit cells remains.
The eigenvalue equation for this matrix gives even and odd recursion equations,
Note that the geometric mean of the masses is a factor of 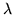 in both equations. To avoid square roots, introduce
in both equations. To avoid square roots, introduce
and two wave matrices,
Individually, they define dispersion relations similar to those for the uniform chain, but here it is necessary to evaluate their alternating products, taking into account that they do not commute unless 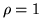 .
.
By symmetry, changing the order of the product would exchange the skewdiagonal elements. Recalling that  has the same eigenvalues as
has the same eigenvalues as 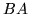 , the dispersion relation is the same for either product, namely
, the dispersion relation is the same for either product, namely
Introduce more abbreviations,
to get the sequence
So the calculation of 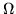 goes pretty much as usual. To get
goes pretty much as usual. To get 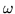 out of
out of 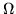 is the interesting part; to simplify formulas still further, define
is the interesting part; to simplify formulas still further, define
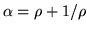 .
.
What really counts is whether
 has to be imaginary or complex, which is best seen by yet another reformulation of the dispersion relation.
has to be imaginary or complex, which is best seen by yet another reformulation of the dispersion relation.
Figure:
heavy and light particles alternate
 |




Next: Tapered string
Up: A Variety of String
Previous: Point defect
Contents
Pedro Hernandez
2004-02-28
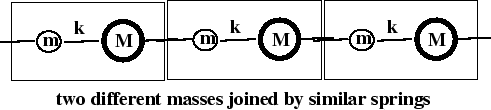
![\begin{eqnarray*}
A & = &
\left[ \begin{array}{cccccc}
\frac{-2k}{m} & \fra...
...urd(m M)} & . \\
. & . & . & . & . & .
\end{array} \right].
\end{eqnarray*}](img483.gif)
![\begin{eqnarray*}
A & = &
\frac{k}{\surd(Mm)}\left[ \begin{array}{cccccc}
-...
...\rho} & 1 & . \\
. & . & . & . & . & .
\end{array} \right].
\end{eqnarray*}](img486.gif)
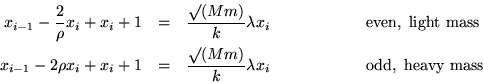
![\begin{eqnarray*}
\left[ \begin{array}{cc}
\omega^2 + \frac{2}{\rho} & -1 \\ ...
...& -1 \\
1 & 0 \end{array} \right] & & {\rm odd,\ heavy\ mass}
\end{eqnarray*}](img489.gif)