Point defect

Figure: Normal modes of a chain of eleven particles with with fixed ends and a point defect consisting of a variant mass.

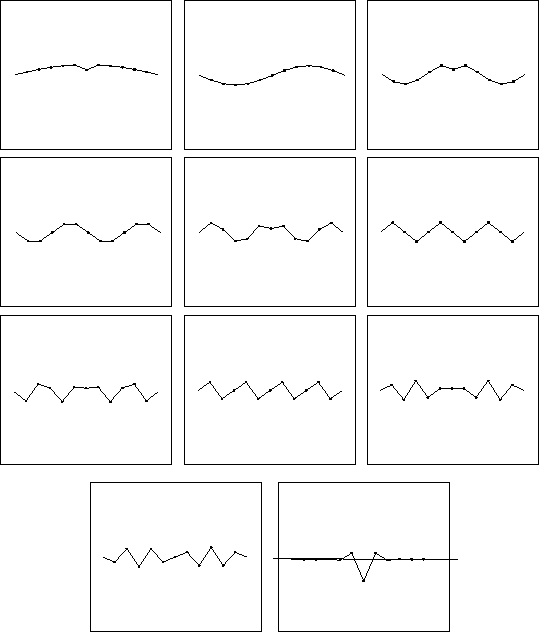The dynamical matrix would look like:

$$\begin{eqnarray*} A & = & \left[ \begin{array}{cccccccccc} \ldots & . & . & ... ...ts & . & . & . & . & . & . & . & . & \ldots \end{array} \right] \end{eqnarray*}$$

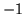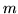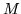with two lines of recursion differing from those in the main body of the matrix. They only affect the wave matrix in the respect that its 12 element is no longer $-1$, but something else. In terms of masses $m$ and $M$, with elastic constants 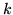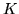$k$, $K$, and an intermediate $k'$, we need

$$\left[ \begin{array}{cc} \frac{\lambda + a + c}{c} & - \fra... ... + a + c}{ c} & - \frac{c}{b} \\ 1 & 0 \end{array} \right]$$

in terms of their eigenvalues and eigenvectors (or else to endure the algebra resulting from using them in their crude form).