


Next: Block Matrices
Up: A Variety of String
Previous: Tapered string
Contents
Figure:
a row of identical masses with identical springs connecting neighbors and another set of springs connecting second neighbors
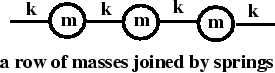 |
The component by component equations for the eigenvectors of a pentadiagonal matrix would have the form
which would turn into recursion relations by writing
and finally an equation with a wave matrix
The characteristic equation for the wave matrix reads
which in turn is a quadratic equation for
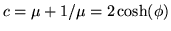 .
.
Pedro Hernandez
2004-02-28
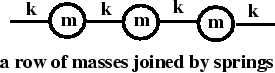
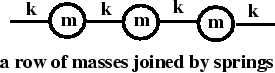
![\begin{eqnarray*}
A & = & \frac{k}{m} \left[ \begin{array}{ccccccccc}
\ldots ...
...ots & . & . & . & . & . & . & . & \cdots
\end{array} \right].
\end{eqnarray*}](img507.gif)
![\begin{eqnarray*}\left[ \begin{array}{c}
x_{i+2} \\ x_{i+1} \\ x_{i} \\ x_{i-1...
...
x_{i+1} \\ x_{i} \\ x_{i-1} \\ x_{i-2}
\end{array} \right].
\end{eqnarray*}](img510.gif)