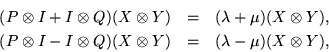


Next: Symmetry
Up: Linear Algebra
Previous: Second neighbor influences
Contents
Matrices sometimes have a structure in which some submatrix is repeated over and over, usually reappearing in the form of different multiples. For example, the product of a column by a row is a rectangular matrix, in which all the rows are proportional, just as the columns are likewise proportional. When the repetition of one matrix is guided by another, the result is sometimes called a KroneckerKronecker product product of the two matrices, and at other times a tensortensor product product. For example, given matrices 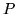 and
and 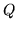 ,
,
their Kronecker product 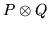 would be defined by
would be defined by
In complete generality, give 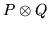 four indices in the form of two pairs, and set
four indices in the form of two pairs, and set
These indices are to be run out in lexicographic order, which means that 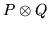 is not the same thing as
is not the same thing as 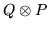 , although it is equivalent
by a change of basis which permutes the indices.
, although it is equivalent
by a change of basis which permutes the indices.
Calculation with Kronecker products is facilitated by verifying all the algebraic rules, such as distributivity or associativity, which they obey, thereafter using them automatically. Let 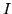 stand for a unit matrix,
stand for a unit matrix, 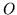 zero matrices of the appropriate size and shape,
zero matrices of the appropriate size and shape, 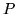 ,
, 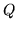 and
and 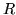 generic matrices.
As needed,
generic matrices.
As needed, 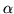 and
and 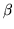 could be scalar factors. Then
could be scalar factors. Then
Apparently a Kronecker product resembles a cartesian product, in the sense that the factors combine fairly independently when it comes to mingling the Kronecker product with other operations such as linear combination or matrix multiplication. Some further results are useful; if the factors are invertible,
wherein it should be noted that the order of the factors is preserved.
If there are eigenvectors 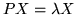 and
and 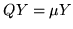 ,
,
This means that the Kronecker product has all possible products of eigenvalues associated with all possible Kronecker products of eigenvectors, due regard being given to the possibility of Jordan normal forms, and with similar results whenever they occur. Beyond that, under the same assumptions,
which provides a matrix with all the possible sums, or all the possible differences, of the eigenvalues of two given matrices as its own eigenvalues. Checking whether the second combination were singular would tell immediately whether a pair of matrices had common eigenvalues.



Next: Symmetry
Up: Linear Algebra
Previous: Second neighbor influences
Contents
Pedro Hernandez
2004-02-28
![]() and
and ![]() ,
,
![\begin{eqnarray*}
P \otimes Q & = & \left[ \begin{array}{cc}
a Q & b Q \\ c Q...
...cA & cB & dA & dB \\
cC & cD & dC & dD
\end{array} \right].
\end{eqnarray*}](img516.gif)
![\begin{eqnarray*}
\left[ \begin{array}{cccc}
aA & aB & bA & bB \\
aC & aD &...
...
aC & bC & aD & bD \\
cC & dC & cD & dD
\end{array} \right]
\end{eqnarray*}](img519.gif)
![]() stand for a unit matrix,
stand for a unit matrix, ![]() zero matrices of the appropriate size and shape,
zero matrices of the appropriate size and shape, ![]() ,
, ![]() and
and ![]() generic matrices.
As needed,
generic matrices.
As needed, ![]() and
and ![]() could be scalar factors. Then
could be scalar factors. Then
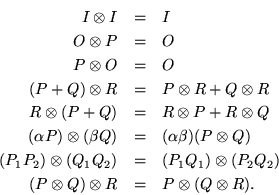
![]() and
and ![]() ,
,