Groups

A collection of symmetries has the important property of forming a groupgroup. That is, if $A S = S A$ and $A T = T A$, then

$$\begin{eqnarray*} A(ST) & = & (AS) T \\ & = & (SA) T \\ & = & S (AT) \\ & = & S (TA) \\ & = & (S T) A \end{eqnarray*}$$

This derivation is pretty detailled, but such meticulous attention to detail is usual when working with the axiomatics of groups. Its conclusion is that the product of two matrices which commute with a third also commutes with the third, which is the closure requirement in the definition of a group.

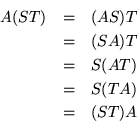
Altogether, the definition of a group requires a collection of objects and a binary operation, called mutiplication for the sake of argument, which associates a third element with a given pair. The postulates for group multiplication are

closure

multiplication is defined for all pairs,

associativity

multiplication is associative: $a(bc) = (ab)c$,

left identity

there is an element $e$ for which $e a = a$, whatever $a$,

left inverse

for every $a$, there is a $b$ satisfying $b a = e$.

As usual with concise mathematical statements, some reassurance often improves understanding. For example, insisting on one identity does not of itself preclude there being others; however that is the one which should be used in applying the fourth postulate.

If the statement of the postulates appears a little strange, that is because they are usually given in both a strong form and a weak form. The advantage of the weak form, with left identities, left inverses (the handedness does have to be the same), and no mention of uniqueness, is that there is less to verify while recognizing a group. But there is sufficient information present to show that uniqueness holds, that the identity and inverses work from both sides, useful relationships such as $(ab)^{-1} = b^{-1}a^{-1}$ or $(a^{-1})^{-1} = a$, and that equations are always solvable.

This latter property, that $ax=b$ has the unique solution $x=a^{-1}b$, is probably the one most responsible for the importance of the group concept.

Groups are excellent objects to which to apply the mathematical theory of structures, so it is convenient to recognize subgroups, factor groups, and product groups.