



Next: Groups
Up: Symmetry
Previous: wave matrices
Contents
What we have worked out are the consequences for the wave matrix of a reflective symmetry. Rather than leaving the wave matrices unchanged, it turns them into their inverses. It is the dynamical matrix which should be unchanged. Let
Then  , every element is reflected across the center of the matrix, and remains unchanged. That means for all eigenvectors X,
, every element is reflected across the center of the matrix, and remains unchanged. That means for all eigenvectors X,
Thus either 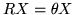 and
and 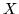 is an eigenvector of
is an eigenvector of  (when two matrices commute, they have common eigenvectors) or else
(when two matrices commute, they have common eigenvectors) or else 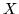 and
and 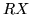 are two linearly independent eigenvectors belonging to the same eigenvalue of
are two linearly independent eigenvectors belonging to the same eigenvalue of 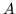 . Of course, it might also happen that
. Of course, it might also happen that 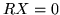 . Here,
. Here, 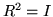 , so
, so 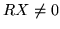 . Neither is it possible to go on finding still more eigenvectors belonging to the common eigenvalue.
. Neither is it possible to go on finding still more eigenvectors belonging to the common eigenvalue.
In other words symmetry
implies degeneracy
Conversely, an appeal to Sylvester's theorem shows that forming linear combinations of degenerate eigenvectors should commute with 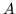 and so should induce a symmetry. Clearly the size and number of degenerate subspaces depends on the action of
and so should induce a symmetry. Clearly the size and number of degenerate subspaces depends on the action of  , and it is evidently a mutual relationship.
, and it is evidently a mutual relationship.
Continuing to think of the dynamical matrix for the vibrations of a string, the influence of reflective symmetry is that for every normal mode, the reflection has to be another normal mode. That doesn't actually produce nodes of different shape; because 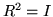 , its eigenvalues are
, its eigenvalues are 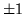 , making normal modes either even (and hence unchanged) or odd with respect to reflection. In general, half the sum and half the difference of any mode and its reflection would be eigenvectors of the reflection.
, making normal modes either even (and hence unchanged) or odd with respect to reflection. In general, half the sum and half the difference of any mode and its reflection would be eigenvectors of the reflection.
Cyclic chains have another symmetry, which is shifting from one particle to the next:
because 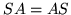 . In fact,
. In fact, 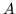 is a function of
is a function of 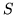 , given that
, given that
That means the cyclic shift of any normal mode has to be another normal mode of the same frequency. The relationship is less obvious than the one resulting from reflection, because 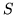 has complex eigenvalues and eigenvectors. Recall that when diagonizable matrices commute we have to find a set of mutual eigenvectors so that both will be diagonal in the same coordinate system. The symmetry shows up through the use of sines and cosines to describe the normal modes rather than complex exponentials. As the situation is usually described, the normal modes are standing waves rather than travelling waves.
has complex eigenvalues and eigenvectors. Recall that when diagonizable matrices commute we have to find a set of mutual eigenvectors so that both will be diagonal in the same coordinate system. The symmetry shows up through the use of sines and cosines to describe the normal modes rather than complex exponentials. As the situation is usually described, the normal modes are standing waves rather than travelling waves.
Altogether the cyclic string has two symmetries,  and
and 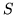 , and they don't commute with one another:
, and they don't commute with one another:
 . This lack of commutation obliges
. This lack of commutation obliges 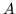 to have multiple eigenvalues, because of the difficulty in finding vectors which are sumultaneously eigenvectors of
to have multiple eigenvalues, because of the difficulty in finding vectors which are sumultaneously eigenvectors of 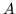 ,
,  , and
, and 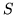 . The condition of degeneracy is sufficient, but for particular combinations there could be still further degeneracies which were not based on the shifting of the eigenvectors of one of the matrices by the others.
. The condition of degeneracy is sufficient, but for particular combinations there could be still further degeneracies which were not based on the shifting of the eigenvectors of one of the matrices by the others.




Next: Groups
Up: Symmetry
Previous: wave matrices
Contents
Pedro Hernandez
2004-02-28
![\begin{eqnarray*}
R & = & \left[ \begin{array}{cccccccc}
\ldots & . & . & . &...
...\
\ldots & . & . & . & . & . & . & \ldots
\end{array} \right]
\end{eqnarray*}](img546.gif)
![\begin{eqnarray*}
R & = & \left[ \begin{array}{cccccccc}
\ldots & . & . & . &...
...\
\ldots & . & . & . & . & . & . & \ldots
\end{array} \right]
\end{eqnarray*}](img546.gif)
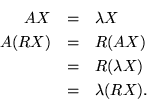
![]() , its eigenvalues are
, its eigenvalues are ![]() , making normal modes either even (and hence unchanged) or odd with respect to reflection. In general, half the sum and half the difference of any mode and its reflection would be eigenvectors of the reflection.
, making normal modes either even (and hence unchanged) or odd with respect to reflection. In general, half the sum and half the difference of any mode and its reflection would be eigenvectors of the reflection.
![\begin{eqnarray*}
S & = & \left[ \begin{array}{cccccccc}
\ldots & . & . & . &...
...\\
\ldots & . & . & . & . & . & . & \ldots
\end{array} \right] \end{eqnarray*}](img556.gif)
![]() and
and ![]() , and they don't commute with one another:
, and they don't commute with one another:
![]() . This lack of commutation obliges
. This lack of commutation obliges ![]() to have multiple eigenvalues, because of the difficulty in finding vectors which are sumultaneously eigenvectors of
to have multiple eigenvalues, because of the difficulty in finding vectors which are sumultaneously eigenvectors of ![]() ,
, ![]() , and
, and ![]() . The condition of degeneracy is sufficient, but for particular combinations there could be still further degeneracies which were not based on the shifting of the eigenvectors of one of the matrices by the others.
. The condition of degeneracy is sufficient, but for particular combinations there could be still further degeneracies which were not based on the shifting of the eigenvectors of one of the matrices by the others.