Convolutionconvolution algebra algebra

Consider a collection of mappings from a group, regarded as a point set, to the complex numbers. Actually, any field would do, but choosing the complex numbers gives results of wide and common applicability. Such a collection of mappings is reminiscent of the dual space for a vector space and it will be seen that the theories follow quite similar lines. It always seems to be advantageous to work with the functions of a point set in place of the set itself.

Characteristic functions of subsets follow the definition:

$$\begin{eqnarray*} \delta(S;x) & = & \left\{ \begin{array}{ll} 1 & x \varepsilon S \\ 0 & {\rm otherwise} \end{array} \right. \end{eqnarray*}$$

Amongst the characteristic functions, those of the unit classes constitute a basis because any function 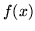$f(x)$ can be written

$$\begin{eqnarray*} f(x) & = & \sum_{g\varepsilon G} f(g) \delta(g;x). \end{eqnarray*}$$

Linear combinations and products of functions are to be defined as usual,

$$\begin{eqnarray*} (\alpha f + \beta g)(x) & = & \alpha f(x) + \beta g(x), \\ (fg)(x) & = & f(x) g(x). \end{eqnarray*}$$

So far nothing remarkable has been produced, but the influence of group nultiplication has not yet been felt. That results from defining the convolution of two functions,

$$\begin{eqnarray*} f*g(x) & = & \sum_{ab=x} f(a) g(b). \end{eqnarray*}$$

It results that 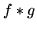$f*g$ is not necessarily commutative, but that it is bilinearly distributive and associative.