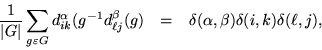There are now two ways to get a matrix representation of a the group multiplication, according to whether the characteristic functions are used as left factors or as right factors for a convolution. In each case, the other factor is expanded in a basis as though it were a vector. For the left regular representation,

Consider that a representationgroup representation is given, a set of matrices
![]() for which
for which
![]() , and look at the matrix elements
, and look at the matrix elements ![]() . These are complex valued functions of the group elements and thereby subject to the preceding formula:
. These are complex valued functions of the group elements and thereby subject to the preceding formula:
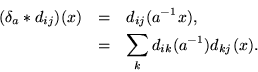
We need to know whether the matrices of ![]() are diagonal or not and if not, to what extent. Recall that matrices commute when they have common eigenvectors, and hence can be chosen to be diagonal, all of them at once. If any matrix but a multiple of the identity commutes with all the matrices of
are diagonal or not and if not, to what extent. Recall that matrices commute when they have common eigenvectors, and hence can be chosen to be diagonal, all of them at once. If any matrix but a multiple of the identity commutes with all the matrices of ![]() , and that multiple can be diagonalized with two different eigenvalues, all the matrices of
, and that multiple can be diagonalized with two different eigenvalues, all the matrices of ![]() must follow suit.
must follow suit.
Therefore, if all of ![]() cannot be placed in the form of diagonal blocks by some choice of coordinates, the matrix which commutes with all of them must be a multiple of the identity, a result which is known as Schur'sSchur's lemmas first lemma. His second lemma relates to the possibility of forming an equivalence between two different matrix representations
cannot be placed in the form of diagonal blocks by some choice of coordinates, the matrix which commutes with all of them must be a multiple of the identity, a result which is known as Schur'sSchur's lemmas first lemma. His second lemma relates to the possibility of forming an equivalence between two different matrix representations ![]() and
and ![]() . Give the matrices identifying superscripts and suppose a matrix
. Give the matrices identifying superscripts and suppose a matrix ![]() for which, whatever group element,
for which, whatever group element,
On the other hand, if ![]() is not zero, there will be a row such that
is not zero, there will be a row such that ![]() is non-zero; it just needs a
is non-zero; it just needs a ![]() in a strategic place to take advantage of one of
in a strategic place to take advantage of one of ![]() 's non-sero elements.
's non-sero elements.
Finally, consider that neither ![]() nor
nor ![]() are singular (we really wouldn't want to consider a set of zero matrices a representation) because
are singular (we really wouldn't want to consider a set of zero matrices a representation) because
![]() and every group element has an inverse.
and every group element has an inverse.
Therefore ![]() cannot map a non-zero vector into zero, so
cannot map a non-zero vector into zero, so ![]() is nonzero, contradicting the vanishing of
is nonzero, contradicting the vanishing of ![]() . So
. So ![]() would have to vanish in its entirety, which is the statement of Schur's second lemma.
would have to vanish in its entirety, which is the statement of Schur's second lemma.
There is a little more to be said because ![]() could be square, leaving the existence of
could be square, leaving the existence of ![]() in question. If there were such an
in question. If there were such an ![]() ,
, ![]() would still be singular and would need to vanish, leading to the same conclusion. If, on the contrary,
would still be singular and would need to vanish, leading to the same conclusion. If, on the contrary, ![]() were invertible, the representations
were invertible, the representations ![]() and
and ![]() would have to be equivalent so the only possibility for inequivalent representations, even of the same dimension, would be
would have to be equivalent so the only possibility for inequivalent representations, even of the same dimension, would be ![]() .
.
In summary, a representation is irreducible when there is no choice of basis where all its matrices are simultaneously partitioned into diagonal nonzero blocks. Of course, some of of the individual matrices, such as the identity matrix representing the identity element, may well be reduced; but not all of them in the same way at once. If only the zero equivalence can connect two representations, they are inequivalent, and if they are both the same representation, only a multiple of the identity can connect them.
Averaging over a group yields a plentiful supply of equivalences, depending upon what is averaged. Define ![]() , for any matrix
, for any matrix ![]() compatible with the two dimensions,
compatible with the two dimensions,
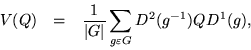
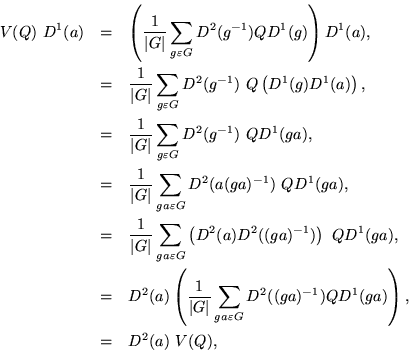
Dividing the sum by the order of the group was really unnecessary, but it will be convenient later on. For example, if ![]() and the same representation is used both times, the result will be
and the same representation is used both times, the result will be ![]() . Accordng to Schur's lemma, after adorning V with superscripts to trace its definition and inventing a sort of generic Kronecker delta for matrices,
. Accordng to Schur's lemma, after adorning V with superscripts to trace its definition and inventing a sort of generic Kronecker delta for matrices,