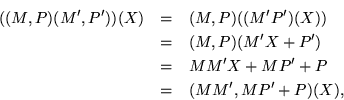Affine space

The semidirect product of groups was known to crystallographers and others as the way to describe the symmetry group of a lattice, long before the idea was taken up by mathematicians in the 1950's. The concept arises from combining lattice symmetry expressed by the addition of translation vectors with point symmetry implemented using matrices rotating or reflecting the vectors displacing unit cells.

Written in terms of components, a typical formula $X' = M X + P$ would read

$$\begin{eqnarray*} \left[ \begin{array}{c} x' \\ y' \end{array} \right] & = & ... ...\left[ \begin{array}{c} ax+by+p \\ cx+dy+q \end{array} \right]. \end{eqnarray*}$$

Such a mapping of a vector space is called an affine transformation, to distinguish it from a linear transformation; note that

$$\begin{eqnarray*} M (\alpha X + \beta Y) + P & = & M \alpha X + M \beta Y + P \\ & \neq & \alpha (M X + P) + \beta (M Y + P), \end{eqnarray*}$$

so that $P$ appears only once in the result and it isn't scaled at all. Although the mapping isn't linear, it is certainly useful, which invites the study of its properties.

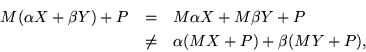
One of them is the rule of composition. Suppose that we regard the pair $(M,P)$ as the cartesian product of two functions, and apply two such pairs in succession to a vector X, and take due note of the confusion arising from using parentheses to define a compound function on the one hand, and their normal use to group terms within an algebraic expression. Then

$$\begin{eqnarray*} ((M,P)(M',P'))(X) & = & (M,P)((M'P')(X)) \\ & = & (M,P)(M'X+P') \\ & = & MM'X + MP' + P \\ & = & (MM',MP'+P)(X), \end{eqnarray*}$$

which is the rule of composition for the two mappings.