Projective space

The projective viewpoint would regard the defining equation $X' = M X + P$ as a fragment of a partitioned matrix equation:

$$\begin{eqnarray*} \left[ \begin{array}{c} \xi' \\ \eta' \\ \hline \zeta' \end{a... ...egin{array}{c} \xi \\ \eta \\ \hline \zeta \end{array} \right]. \end{eqnarray*}$$

The componentwise equations,

$$\begin{eqnarray*} \xi' & = & a \xi + b \eta + p \zeta \\ \eta' & = & c \xi + d \eta + q \zeta \\ \zeta' & = & 0 \xi + 0 \eta + 1 \zeta \end{eqnarray*}$$

could be reconciled with the earlier equations by introducing the mapping

$$\begin{eqnarray*} x = \frac{\xi}{\zeta} \\ y = \frac{\eta}{\zeta} \end{eqnarray*}$$

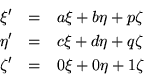
Projective geometry is more comprehensive than affine geometry because there is no reason to restrict the transformation matrix to be upper triangular. If the more elaborate matrix

$$\left[ \begin{array}{cc\vert c} a & b & p \\ c & d & q \\ \hline r & s & w \end{array} \right]$$

were used, the projective transformation would read

$$\begin{eqnarray*} x' & = & \frac{ax + by + p}{rx + sy + w} \\ y' & = & \frac{cx + dy + q}{rx + sy + w}. \end{eqnarray*}$$

A special case would include uniform dilation

$$\begin{eqnarray*} x' & = & \lambda x \\ y' & = & \lambda y. \end{eqnarray*}$$

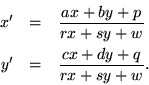
Generally speaking, a linear transformation of $n$ coordinates can be mapped into a projective transformation of $(n-1)$ coordinates, and conversely a nonlinear transformation of $n$ coordinates having the projective form can be mapped into a linear transformation of $n+1$ coordinates. In neither case is the transformation one-to-one, since all multiples of a vector have a common projective image, just as the counterimage of a projection has to include all multiples of any one of its points.