Mappings of a line

Related to the question of discovering and describing linear and projective mappings is the related question of whether mappings are invertible or not. That depends to a certain extent on how the function is described - that is, whether it is a polynomial, rational fraction, or specified in some much more general context. In general calculus, if a set of functions $y_i(x_1, x_2, \ldots, x_n)$ have derivatives, the differential relationships

$$\begin{eqnarray*} dy_1 & = & \frac{\partial y_1}{\partial x_1} dx_1 + \frac{\... ...l x_2} dx_2 + \ldots + \frac{\partial y_n}{\partial x_n} dx_n \end{eqnarray*}$$

have a matrix formulation

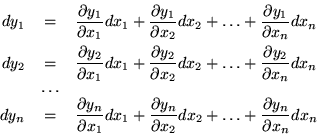
$$\begin{eqnarray*} \left[ \begin{array}{c} dy_1 \\ dy_2 \\ \ldots \\ dy_n \end{a... ...in{array}{c} dx_1 \\ dx_2 \\ \ldots \\ dx_n \end{array} \right] \end{eqnarray*}$$

in which the matrix could be called a JacobianJacobian determinant matrix in analogy to the well-known Jacobian determinant. Actually there is a similar set of equations, using the transposed Jacobian matrix, relating partial derivatives with respect to one set of variables to those with respect to another. In either event, the nonvanishing of the Jacobian determinant is the criterion for local invertibility of the set of mappings. Less commonly discussed is whether the Jacobian matrix has eigenvalues and eigenvectors, although it would seem that they could surely provide further information concerning the local nature of the mapping.

Such general criteria provide only local information, although conclusions could be drawn from the nonsingularity of the Jacobian determinant over entire regions. Suppose, however, that the variables are related in a more implicit form, by the vanishing of a series of polynomial equations, and that to confine the discussion to the simplest case, that just the variables $x$ and $y$ are so related. Then the coefficients of powers of $y$ could be gathered together to make up a polynomial in $y$ whose roots would imply that several combinations of $x$ and constant coefficients producing the same value for $y$. To avoid that eventuality, no powers of $y$ should occur - just $y$ itself and terms independent of $y$.

By symmetry, the same could be said of $x$. Only the meagre possibility

$$a x y + b x + c y + d = 0$$ (2)

remains, which could be rendered explicit in either one of the two forms

$$\begin{eqnarray*} x & = & -\frac{cy+d}{ay+b} \\ y & = & -\frac{bx+d}{ax+c} \end{eqnarray*}$$

Both of these expressions look like one-dimensional projective transformations of an affine plane; if they were written in matrix form there would result

$$\begin{eqnarray*} \left[ \begin{array}{c} x \\ 1 \end{array} \right] & = & \l... ...ray} \right] \left[ \begin{array}{c} x \\ 1 \end{array} \right] \end{eqnarray*}$$

This matrix form, while not unique, reveals the convenience of a nonvanishing determinant $ad-bc$; otherwise $x$ would have a value independent of $y$ and conversely. Neither would yield the single valued mapping we are looking for.

The matrices, except for the determinantal factor and the placement of some signs, are inverses, forerunning the observation that functional composites follow the rules of matrix multiplication. Since a quotient is involved, or otherwise stated, the original equation is homogeneous with respect to the coefficients, multiplying the matrices by a factor could give them a unit determinant, so the transformation can always be represented by unimodular matrices. To ensure the validity of matrix multiplication for their representation, the coefficients should always be arranged as shown, not reversed. In fact, it is worth looking at the substitution in detail, paying attention to the direction of the mapping, the direction of composition, and the placement of the coefficients in the matrix. If it were given, following the representation of x as a function of y, a sequence of two mappings,

$$\begin{eqnarray*} x & = & \frac{-cy-d}{ay+b} \\ w & = & \frac{-Cx-D}{Ax+B} \end{eqnarray*}$$

then substitution would say

$$\begin{eqnarray*} w & = & \frac{-C\left(\frac{-cy-d}{ay+b}\right)-D} {A\left(\... ...)+B(ay+b)} \\ & = & \frac{(Cc-Da)y-(cD-Db)}{(-Ac+Ba)y+(Ad+Bb)} \end{eqnarray*}$$

which would correspond to a matrix product

$$\begin{eqnarray*} \left[ \begin{array}{cc} -C & -D \\ A & B \end{array} \right]... ...y}{cc} Cc-Da & -(Cd-Db) \\ -AC+Ba & Ab+Bb \end{array} \right] \end{eqnarray*}$$

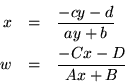
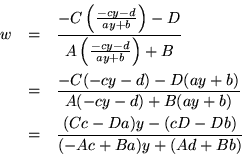
The conclusion of this line of analysis is that under very general conditions -- namely implicit representation by coefficients of a vanishing polynomial -- the only invertible mapping of a line into itself is a projective transformation. Note that projective transformations are slightly more general than affine transformations (but only slightly) because projection from a linear space envisions not just one affine transformation, but even a quotient of two of them.