Fixed points for projective mappings

Figure: Elliptic trajectories run around circles surrounding one of the fixed points. Hyperbolic tranectories run along circular arcs connecting the two fixed points, away from one towards the other. Parabolic trajectories arise when the two fixed points coalesce, in which case the two families of orbits look the same, just rotated $90^o$.

A fixed point should satisfy the equation (assuming $ad-bc=1$)

$$\begin{eqnarray*} x & = & \frac{ax+b}{cx+d} \\ & = & \frac{(a-d)\pm\surd((d+a)^2-1)}{2c}. \end{eqnarray*}$$

These fixed points are not the eigenvalues of the matrix of the mapping, but rather its eigenvectors. Although the eigenvalues are not directly evident, they still enter into the dynamics of the mapping.

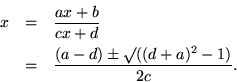
Given their representation as unimodular matrices, the transformations follow an Euler formula with a unit vector and angle of hyperbolic rotation. If the angle is real, the fixed points are real, describing motion from one real fixed point toward the other; if it is imaginary there is no real fixed point. Which of the two cases depends on the size of $a+d$.

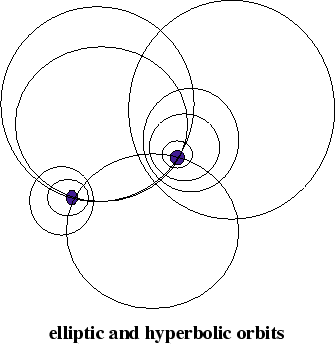
Of course, for a complex line, there are always fixed points. If the fixed points were zero and infinity, the hyperbolic mappings would be contractions or dilations. If the eigenvalue were imaginary, the elliptic mappings would be rotations about the origin. In either case they could be raised to integer, or even rational or real powers, sweeping out either radial arcs or curcular arcs, which could be considered as trajectories of the mapping.

For other pairs of fixed points, the trajectories would be the images of circles (radii, and straight lines in general, are circles through infinity), and so themselves circles positioned with respect to the fixed points. Elliptical orbits encircle the fixed points, hyperbolic orbits ooze from the vicinity of one fixed point toward the vicinity of the other, again along circular arcs.