Functions of cartesian products

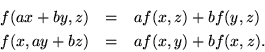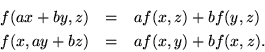
Before cartesian products were mentioned, vector spaces already had a collection of attributes, such as bases, dual spaces, and the dual basis. Since cartesian products of vector spaces are vector spaces in their own right, curiosity would imply examine relationships between the product space and the factors. For example, the cartesian product of bases could be a basis for the cartesian product, but is it true that any basis for a cartesian product can be factored into a product of bases?

Just as there are cartesian products of sets, there should be cartesian products of functions. Directly interpreting such an idea, any product function applied to a cartesian product of arguments ought to produce a cartesian product of values.

However, there are less ambitious functions for product spaces than either of these two possibilities. Consider a scalar valued function of a pair of vectors which is linear separately for each term, rather than being required to be jointly linear:

$$\begin{eqnarray*} f(a x + b y, z) & = & a f(x, z) + b f(y, z) \\ f(x, a y + b z) & = & a f(x, y) + b f(x, z). \end{eqnarray*}$$

The main difference is that we want either $a f(x, y) = f(a x, y)$ or $a f(x, y) = f(x, ay)$, but not at all $a f(x, y) = f(a x, a y)$, which it would have to be if $(x, y)$ were a vector on which $f$ were operating linearly. According to the modest definition, we would have $f(a x, a y) = a^2 f(x, y)$.