Equivalence Relations

Presumably there are linear mappings between any pair of vector spaces; certainly the zero map always exists. If the spaces have different dimensions some discrepancies are bound to occur, because not even the basis vectors can be matched up one-to-one, much less all the rest of the vectors. One use of equivalence relations is to clarify the relatioship between two spaces connected by a function, because the sets where the function takes a constant value are equivalence classes. General properties of equivalence relations are thereby transferred into general relationships among functions.

Figure: Equivalence relations is a linear mapping

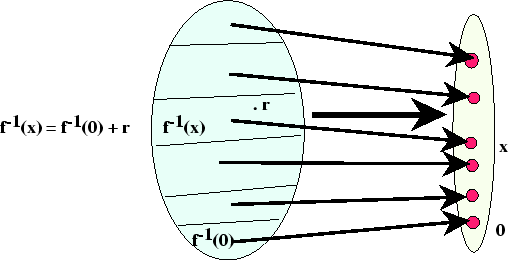
To begin with, all the counterimages of a linear mapping depend on the counterimage of zero. Suppose that $f(r) = x$ and $f(s) = x$ as well. Then

$$\begin{eqnarray*} f(r - s) & = & f(r) - f(s) \\ & = & x - x \\ & = & 0, \end{eqnarray*}$$

placing the difference of any pair of elements with a common image amongst the elements which map into zero. That is enough to make the counterimage of zero, which is usually called the kernel of the mappping, into a vector space, and to make all the other equivalence classes differ from it by translation. As an example, think of orthogonal projection mapping space onto the x-y plane. The z-axis is the kernel of the mapping whose translates are the vertical lines containing the counterprojections of any other point.

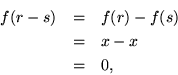
In passing, note that both the images and the counterimages of vector spaces are vector spaces, according to a linear mapping. As far as the vector spaces themselves are concerned, that is nothing but the definition of linear mapping. But it automatically carries over to all the subspaces as well, which is the useful part of the remark. Besides which, the multiplicity of counterimages is uniform everywhere, giving vector space theory an elegance which is not shared by all mathematical structures.

The functions in the dual space, unless they are zero, have to map onto a one-dimensional space because that is all there is. Each basis function maps its counterpart's multiples to the full coefficient space, leaving the space spanned by all the remaining basis vectors for its kernel. Altogether, the dual basis allocates each vector a line and a hyperplane omitting that line (but only because the basis was there already).