Next: Bibliografía Up: Aproximación de e^z a Previous: Planteamiento

Análisis

Una de las propiedades de e^z es:

e^z₁e^z₂ = e^z₁+z₂

En particular se cumple que:

e^ze^-z = e^z-z = e⁰ = 1

como z es cualquier número complejo del resultado anterior y del teorema que dice que el producto de dos números complejos es igual a cero, sí y sólo si, al menos uno de los factores es cero, tenemos que e^z no es igual a cero.

Por lo estipulado en el párrafo anterior se da respuesta a la pregunta a) e i), e^z no tiene ceros y por lo tanto no pueden coincidir con los del polinomio de Taylor que la aproxima.

La pregunta b) se basa en el resultado conocido como Teorema Fundamental del Álgebra (TFA) que dice:

Si P es un polinomio de grado $n \geq 1$ , entonces P(x) = 0 tiene cuando menos una raíz (posiblemente compleja).

Corolario

Si $P(x) = a_nx^n+a_{n-1}x^{n-1}+ \cdots +a_1x+a_0$ es un polinomio de grado $n \geq 1$ , entonces existen constantes únicas x₁, x₂, ... , x_k, posiblemente complejas, y enteros positivos, m₁, m₂,..., m_k tales que $\sum_{i=1}^k m_i=n$ y

$\begin{displaymath}P(x) = a_n(x-x_1)^{m_1}(x-x_2)^{m_2} \cdots (x-x_k)^{m_k}\end{displaymath}$

El TFA junto con el corolario nos dice que, todo polinomio con coeficientes complejos tiene n raíces (posiblemente complejas).

Del TFA y de la respuesta de a) nos ha llevado a la pregunta ii).

La pregunta iii) es importante ya que nos podría aclarar el comportamiento del polinomio en general.

Para dar respuesta a ii) y iii) se realizó con la ayuda del programa de graficación PLOT en la versión en lenguaje `C', los programas pexp.c, cmuller.c, gemc.c, gep.c y empleando las microcomputadoras tipo PC y los graficadores Hiplot DMP-29 del Departamento de Aplicación de Microcomputadoras.

La aproximación de la e^z por medio de un pol. de Taylor en el punto 0 es:

$\begin{displaymath}e^{z}=1+z+\frac{z^2}{2!}+\frac{z^3}{3!}+\frac{z^4}{4!}+\frac{z^5}{5!} + \cdots \end{displaymath}$

donde z = x + yi.

La aproximación a e^z es mejor si el grado del polinomio de Taylor es grande. Sin embargo, al realizar la evaluación del polinomio para un grado alto, se tendrán dificultades debido a que intervienen potencias y factoriales cada vez más grandes.

A partir de los polinomios de grado quinto no existen métodos para encontrar las raíces en función de los coeficientes. Las técnicas numéricas se emplean en la resolución de una ecuación cuando la solución exacta no se puede encontrar por métodos algebráicos.

Se inplementó una biblioteca con funciones que manejan números complejos, la cual se integró al programa PLOT.

Se emplea en los programas ``gemc.c'' y ``gep.c'' el método de Gauss con pivoteo parcial, para resolver un sistema de m ecuaciones con n incógnitas.

Se emplea el algoritmo de Horner (división sintética) para la evaluación de los polinomios en un valor dado.

El programa ``pexp.c'' se realizó para obtener la superficie y los contornos de valor absoluto y los contornos de fase de los diferentes polinomios de Taylor que aproximan a e^z, como primer paso para la obtención de las raíces ya que los contornos de fase muestran la región del plano complejo donde se encuentran. Se obtuvieron las gráficas siguientes:

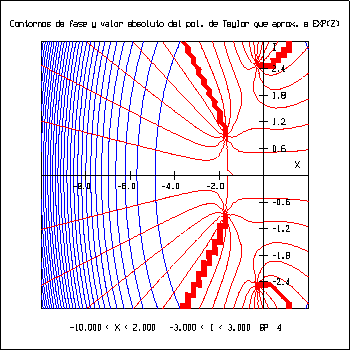
$\begin{figure} \centering \begin{picture} (220,240)(0,0) \put(0,0){\epsfxsize=220pt \epsffile{aecg4.eps}} \end{picture}\end{figure}$

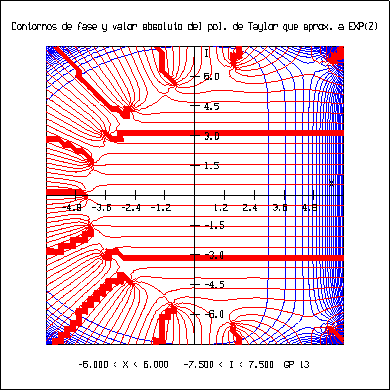
$\begin{figure} \centering \begin{picture} (245,260)(0,0) \put(0,0){\epsfxsize=245pt \epsffile{aecg13.eps}} \end{picture}\end{figure}$

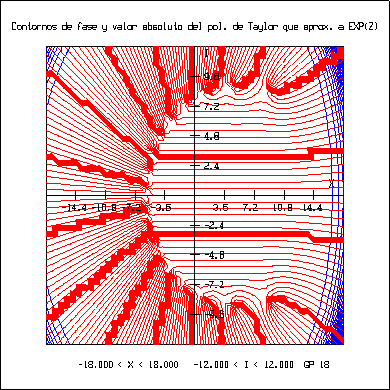
$\begin{figure} \centering \begin{picture} (245,267)(0,0) \put(0,0){\epsfxsize=245pt \epsffile{aecg18.eps}} \end{picture}\end{figure}$

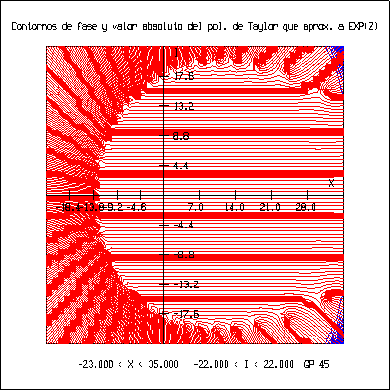
$\begin{figure} \centering \begin{picture} (245,260)(0,0) \put(0,0){\epsfxsize=245pt \epsffile{aecg45.eps}} \end{picture}\end{figure}$

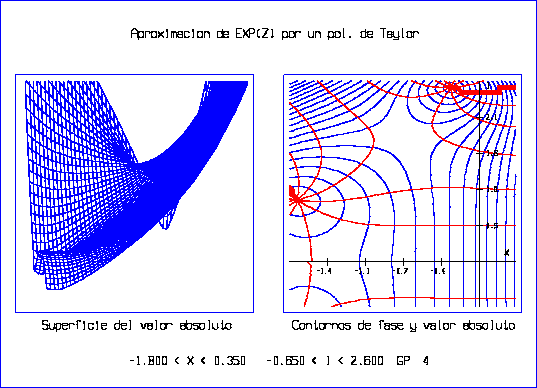
$\begin{figure} \centering \begin{picture} (340,260)(0,0) \put(0,0){\epsfxsize=340pt \epsffile{aepg4.eps}} \end{picture}\end{figure}$

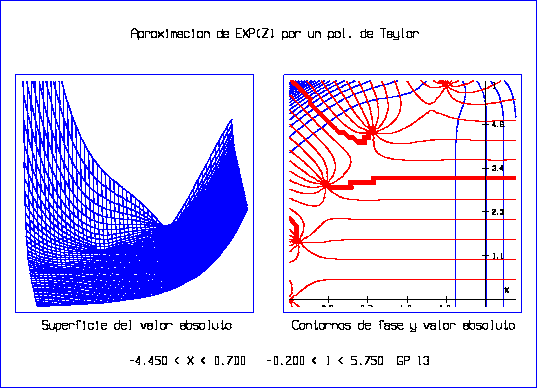
$\begin{figure} \centering \begin{picture} (340,260)(0,0) \put(0,0){\epsfxsize=340pt \epsffile{aepg13.eps}} \end{picture}\end{figure}$

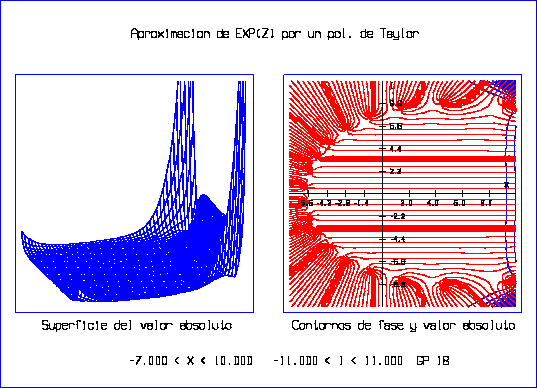
$\begin{figure} \centering \begin{picture} (340,260)(0,0) \put(0,0){\epsfxsize=340pt \epsffile{aepg18.eps}} \end{picture}\end{figure}$

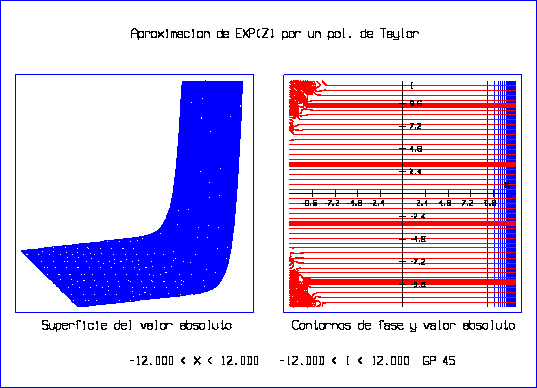
$\begin{figure} \centering \begin{picture} (340,260)(0,0) \put(0,0){\epsfxsize=340pt \epsffile{aepg45.eps}} \end{picture}\end{figure}$

Con la ayuda de las gráficas previas y el programa ``cmuller.c'' se calcularon las raíces del polinomio de Taylor que aproxima a la exponencial.

El programa ``cmuller.c'' encuentra una raíz compleja de un polinomio por el Método de Müller, solicita se le proporcione una aproximación a la raíz, la cual se puede obtener al observar los contornos de fase generados por el programa ``pexp.c''.

El método de Müller usa tres aproximaciones iniciales x₀, x₁ y x₂ y determina la siguiente aproximación x₃ considerando la intersección del eje x con la parábola que pasa por (x₀,f(x₀)), (x₁, f(x₁)) y (x₂, f(x₂)).

Una vez que se determina x₃, se repite el proceso usando x₁, x₂ y x₃ en lugar de x₀, x₁ y x₂ para determinar la siguiente aproximación x₄. El método continúa hasta que se obtiene una aproximación a la raíz.

La selección de las aproximaciones iniciales no es un factor crítico y se pueden seleccionar cualesquier valores para x₁, x₂ y x₃ siempre que estén cerca del cero. Además con este método se pueden encontrar raíces complejas.

Las raíces son:

        GP  =  1                       GP  =  2

        R1  = -1.0                     R1  = -1.0 + 1.0i
                                       R2  = -1.0 - 1.0i

        GP  = 3                        GP  = 4

        R1  = -1.596072                R1  = -1.729444 + 0.888974i
        R2  = -0.701964 + 1.807339i    R2  = -1.729444 - 0.888974i
        R3  = -0.701964 - 1.807339i    R3  = -0.270556 + 2.504776i
                                       R4  = -0.270556 - 2.504776i

        GP  = 5                        GP  = 6
  
        R1  = -2.180607                R1  = -2.361810 + 0.838350i
        R2  = -1.649503 + 1.693933i    R2  = -2.361810 - 0.838350i
        R3  = -1.649503 - 1.693933i    R3  = -1.441801 + 2.434523i
        R4  =  0.239806 + 3.128335i    R4  = -1.441801 - 2.434523i
        R5  =  0.239806 - 3.128335i    R5  =  0.803612 + 3.697702i
                                       R6  =  0.803612 - 3.697702i

        GP  = 7                        GP  = 8
  
        R1  = -2.759003                R1  = -2.964600 + 0.808878i
        R2  = -2.379884 + 1.628999i    R2  = -2.964600 - 0.808878i
        R3  = -2.379884 - 1.628999i    R3  = -2.286429 + 2.377712i
        R4  = -1.147201 + 3.124039i    R4  = -2.286429 - 2.377712i
        R5  = -1.147201 - 3.124039i    R5  = -0.788794 + 3.771811i
        R6  =  1.406586 + 4.225067i    R6  = -0.788794 - 3.771811i
        R7  =  1.406586 - 4.225067i    R7  =  2.039822 + 4.718615i
                                       R8  =  2.039822 - 4.718615i

        GP  = 9                        GP  = 10
  
        R1  = -3.333551                R1  = -3.553876 + 0.789422i
        R2  = -3.038648 + 1.586801i    R2  = -3.553876 - 0.789422i
        R3  = -3.038648 - 1.586801i    R3  = -3.015536 + 2.335224i
        R4  = -2.110840 + 3.089911i    R4  = -3.015536 - 2.335224i
        R5  = -2.110840 - 3.089911i    R5  = -1.871660 + 3.770190i
        R6  = -0.381070 + 4.384645i    R6  = -1.871660 - 3.770190i
        R7  = -0.381070 - 4.384645i    R7  =  0.066202 + 4.967679i
        R8  =  2.697333 + 5.184162i    R8  =  0.066202 - 4.967679i
        R9  =  2.697333 - 5.184162i    R9  =  3.374870 + 5.626020i
                                       R10 =  3.374870 - 5.626020i

        GP  = 11                       GP  = 12

        R1  = -3.905452                R1  = -4.135608 + 0.775542i
        R2  = -3.664152 + 1.557044i    R2  = -4.135608 - 0.775542i
        R3  = -3.664152 - 1.557044i    R3  = -3.688897 + 2.302757i
        R4  = -2.917051 + 3.056372i    R4  = -3.688897 - 2.302757i
        R5  = -2.917051 - 3.056372i    R5  = -2.757989 + 3.752548i
        R6  = -1.581441 + 4.422355i    R6  = -2.757989 - 3.752548i
        R7  = -1.581441 - 4.422355i    R7  = -1.249125 + 5.049555i
        R8  =  0.546078 + 5.524905i    R8  = -1.249125 - 5.049555i
        R9  =  0.546078 - 5.524905i    R9  =  1.053424 + 6.059491i

        GP  = 11                       GP  = 12

        R10 =  4.069291 + 6.047492i    R10 =  1.053424 - 6.059491i  
        R11 =  4.069291 - 6.047492i    R11 =  4.778196 + 6.451176i
                                       R12 =  4.778196 - 6.451176i


        GP  = 13                       GP  = 14
  
        R1  = -4.475412                R1  = -4.712587 + 0.765103i
        R2  = -4.271244 + 1.534856i    R2  = -4.712587 - 0.765103i
        R3  = -4.271244 - 1.534856i    R3  = -4.330708 + 2.277236i
        R4  = -3.644807 + 3.027344i    R4  = -4.330708 - 2.277236i
        R5  = -3.644807 - 3.027344i    R5  = -3.543834 + 3.731923i
        R6  = -2.548921 + 4.425908i    R6  = -3.543834 - 3.731923i
        R7  = -2.548921 - 4.425908i    R7  = -2.297698 + 5.078392i
        R8  = -0.881341 + 5.654417i    R8  = -2.297698 - 5.078392i
        R9  = -0.881341 - 5.654417i    R9  = -0.483159 + 6.239149i
        R10 =  1.584315 + 6.574007i    R10 = -0.483159 - 6.239149i
        R11 =  1.584315 - 6.574007i    R11 =  2.135677 + 7.070568i
        R12 =  5.499704 + 6.839159i    R12 =  2.135677 - 7.070568i
        R13 =  5.499704 - 6.839159i    R13 =  6.232309 + 7.213148i
                                       R14 =  6.232309 - 7.213148i


        GP  = 15                       GP  = 18
  
        R1  = -5.043887                R1  =  -5.8577  - 0.75037i
        R2  = -4.866962 + 1.517629i    R2  =  -5.8577  + 0.75037i
        R3  = -4.866962 - 1.517629i    R3  =  -5.56162 - 2.23972i
        R4  = -4.327165 + 3.002771i    R4  =  -5.56162 + 2.23972i
        R5  = -4.327165 - 3.002771i    R5  =  -4.95881 - 3.69359i
        R6  = -3.394874 + 4.417704i    R6  =  -4.95881 + 3.69359i
        R7  = -3.394874 - 4.417704i    R7  =  -4.02589 - 5.08382i
        R8  = -2.010333 + 5.711727i    R8  =  -4.02589 + 5.08382i
        R9  = -2.010333 - 5.711727i    R9  =  -2.72141 - 6.3739i
        R10 = -0.058552 + 6.805624i    R10 =  -2.72141 + 6.3739i
        R11 = -0.058552 - 6.805624i    R11 =  -0.97416 - 7.51123i
        R12 =  2.705050 + 7.550940i    R12 =  -0.97416 + 7.51123i
        R13 =  2.705050 - 7.550940i    R13 =   1.34476 - 8.41049i
        R14 =  6.974781 + 7.574562i    R14 =   1.34476 + 8.41049i
        R15 =  6.974781 - 7.574562i    R15 =   4.50281 - 8.90883i
                                       R16 =   4.50281 + 8.90883i
                                       R17 =   9.252   - 8.59442i
                                       R18 =   9.252   + 8.59442i

        GP  = 25                        GP  = 45

        R1  = -7.872305                 R1  = -13.495993    
        R2  = -7.766255 + 1.468153i     R2  = -13.437175 + 1.429999i
        R3  = -7.766255 - 1.468153i     R3  = -13.437175 - 1.429999i   
        R4  = -7.446171 + 2.923836i     R4  = -13.260398 + 2.855943i   
        R5  = -7.446171 - 2.923836i     R5  = -13.260398 - 2.855943i 
        R6  = -6.906072 + 4.353857i     R6  = -12.964656 + 4.273694i 
        R7  = -6.906072 - 4.353857i     R7  = -12.964656 - 4.273694i 
        R8  = -6.135313 + 5.743473i     R8  = -12.548259 + 5.678978i 
        R9  = -6.135313 - 5.743473i     R9  = -12.548259 - 5.678978i 
        R10 = -5.117405 + 7.075286i     R10 = -12.008747 + 7.067274i 
        R11 = -5.117405 - 7.075286i     R11 = -12.008747 - 7.067274i 
        R12 = -3.827918 + 8.327622i     R12 = -11.342847 + 8.433738i 
        R13 = -3.827918 - 8.327622i     R13 = -11.342847 - 8.433738i 
        R14 = -2.230771 + 9.471931i     R14 = -10.546330 + 9.773075i 
        R15 = -2.230771 - 9.471931i     R15 = -10.546330 - 9.773075i 
        R16 = -0.271319 + 10.468207i    R16 =  -9.613880 + 11.079406i
        R17 = -0.271319 - 10.468207i    R17 =  -9.613880 - 11.079406i
        R18 =  2.137688 + 11.256085i    R18 =  -8.538871 + 12.346087i    
        R19 =  2.137688 - 11.256085i    R19 =  -8.538871 - 12.346087i 
        R20 =  5.148669 + 11.735090i    R20 =  -7.313089 + 13.565479i 
        R21 =  5.148669 - 11.735090i    R21 =  -7.313089 - 13.565479i 
        R22 =  9.072662 + 11.711350i    R22 =  -5.926329 + 14.728637i 
        R23 =  9.072662 - 11.711350i    R23 =  -5.926329 - 14.728637i 
        R24 = 14.778359 + 10.692981i    R24 =  -4.365845 + 15.824892i 
        R25 = 14.778359 - 10.692981i    R25 =  -4.365845 - 15.824892i 
                                        R26 =  -2.615537 + 16.841249i 
                                        R27 =  -2.615537 - 16.841249i 
                                        R28 =  -0.654771 + 17.761519i 
                                        R29 =  -0.654771 - 17.761519i 
                                        R30 =   1.543451 + 18.365004i 
                                        R31 =   1.543451 - 18.365004i 
                                        R32 =   4.015429 + 19.224413i 
                                        R33 =   4.015429 - 19.224413i 
                                        R34 =   6.811744 + 19.702392i 
                                        R35 =   6.811744 - 19.702392i 
                                        R36 =  10.006375 + 19.945319i 
                                        R37 =  10.006375 - 19.945319i 
                                        R38 =  13.715056 + 19.871167i 
                                        R39 =  13.715056 - 19.871167i 
                                        R40 =  18.137762 + 19.342547i 
                                        R41 =  18.137762 - 19.342547i 
                                        R42 =  23.680466 + 18.094022i 
                                        R43 =  23.680466 - 18.094022i 
                                        R44 =  31.474447 + 15.453220i 
                                        R45 =  31.474447 - 15.453220i

Analizando las gráficas anteriores y las raíces se concluyó lo siguiente:

Cuando el grado del polinomio de Taylor es par, todas las raíces son complejas.
Cuando el grado del polinomio de Taylor es impar, una raíz es real y las restantes son complejas.
Los ceros reales son negativos.
Los ceros reales se alejan hacia menos infinito conforme el grado del polinomio crece. Por ejemplo:

Grado 1 5 15 25 45

Raíz -1.0 -2.180607 -5.043887 -7.872305 -13.495993
Los ceros complejos se distribuyen simétricamente alrededor del eje real y un poco más de la mitad de ellos tienen parte real negativa.
McIntosh observó que en las gráficas de las superficies de valor absoluto de los diferentes polinomios de Taylor que aproximan a e^z, se observa que el polinomio aproxima a la exponencial adecuadamente dentro del círculo de convergencia de las raíces, fuera del círculo el polinomio toma valores cada vez más grandes y no aproxima a e^z.

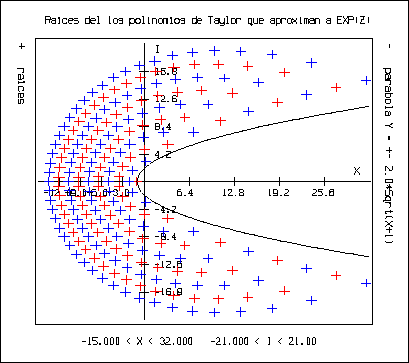
McIntosh comentó que en la Biblioteca del Departamento se encuentra una referencia en la cual se establece que los ceros del polinomio de Taylor que aproxima a e^z tienden a infinito en forma parabólica. Se buscó la referencia pero no se encontró (la búsqueda no fue exhaustiva), por lo que se realizó un programa llamado ``gemc.c'' que ajusta la raíces obtenidas del polinomio de Taylor que aproxima a e^z por el método de mínimos cuadrados con un polinomio de grado dos y grafica éste y las raíces. Se obtuvieron las siguientes gráficas:

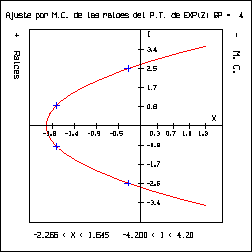
$\begin{figure} \centering \begin{picture} (160,200)(0,0) \put(0,0){\epsfxsize=160pt \epsffile{aemcg4.eps}} \end{picture}\end{figure}$

$\begin{figure} \centering \begin{picture} (220,250)(0,0) \put(0,0){\epsfxsize=220pt \epsffile{aemcg13.eps}} \end{picture}\end{figure}$

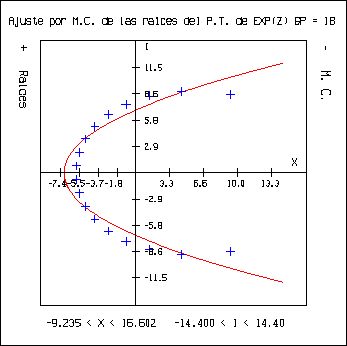
$\begin{figure} \centering \begin{picture} (220,270)(0,0) \put(0,0){\epsfxsize=220pt \epsffile{aemcg18.eps}} \end{picture}\end{figure}$

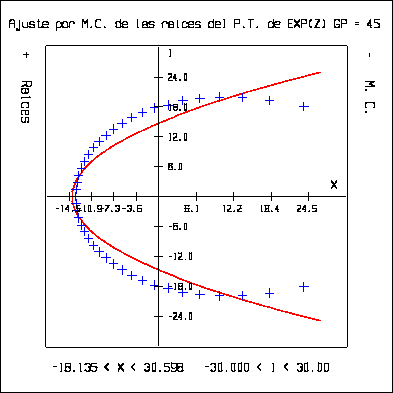
$\begin{figure} \centering \begin{picture} (250,300)(0,0) \put(0,0){\epsfxsize=250pt \epsffile{aemcg45.eps}} \end{picture}\end{figure}$

Analizando las gráficas previas se concluyó que:

El polinomio de mínimos cuadrados de segundo grado únicamente coincide con los polinomios de Taylor de grado tres y cuatro.
En los polinomios de Taylor de mayor grado las raíces complejas con parte real más positiva tienden a cerrar y a no seguir al polinomio de ajuste de mínimos cuadrados.

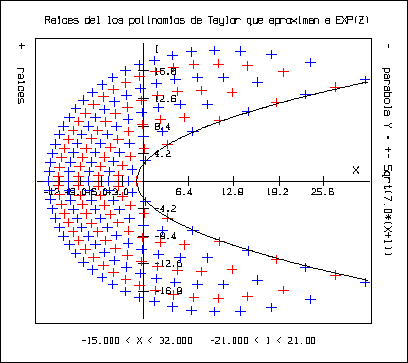
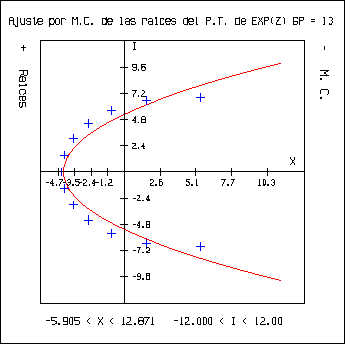
Con respecto al punto anterior, se procedió en otra dirección. Conociendo el eje de la parábola y teniendo tres puntos se puede generar una parábola que pase por los tres puntos. Por lo cual se procedió a tomar las tres raíces que están más cerca del eje real, y tomando el eje real como eje, se generó la parábola que pasa por las tres raíces. Esto se realiza con el programa ``gep.c'' que toma tres de las raíces obtenidas del polinomio de Taylor que aproxima a e^z y traza la parábola que pasa por esos tres puntos. Se obtuvieron las siguientes gráficas:

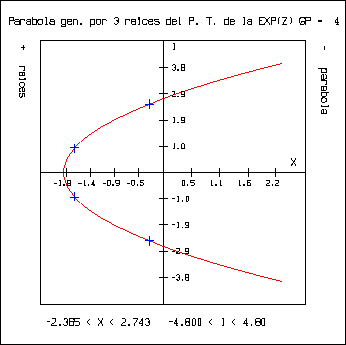
$\begin{figure} \centering \begin{picture} (220,240)(0,0) \put(0,0){\epsfxsize=220pt \epsffile{aepag4.eps}} \end{picture}\end{figure}$

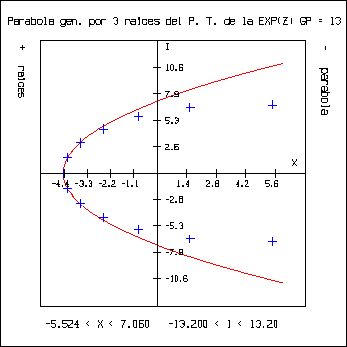
$\begin{figure} \centering \begin{picture} (220,265)(0,0) \put(0,0){\epsfxsize=220pt \epsffile{aepag13.eps}} \end{picture}\end{figure}$

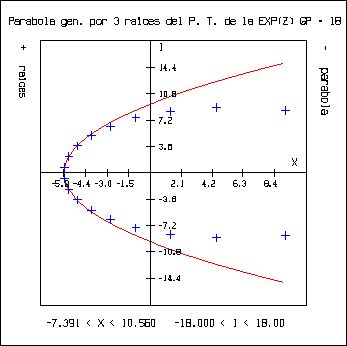
$\begin{figure} \centering \begin{picture} (220,250)(0,0) \put(0,0){\epsfxsize=220pt \epsffile{aepag18.eps}} \end{picture}\end{figure}$

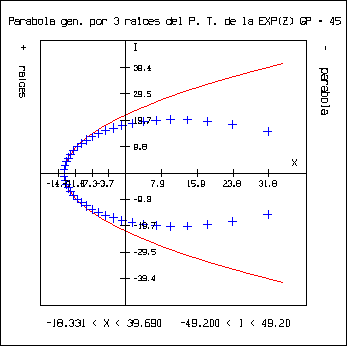
$\begin{figure} \centering \begin{picture} (220,269)(0,0) \put(0,0){\epsfxsize=220pt \epsffile{aepag45.eps}} \end{picture}\end{figure}$

Con respecto a estas gráficas podemos decir:

Las gráficas muestran que la raíces caen dentro de la parábola generada y que no la ajustan adecuadamente. Sin embargo, se puede pensar en un comportamiento asintótico de las raíces con respecto a la parábola.
Las raíces del polinomio de Taylor que tienen mayor desviación de la parábola, podrían indicar que posiblemente había errores de redondeo y de truncamiento en la evaluación del polinomio.

Con respecto al último punto se decidió emplear el programa Mathematica para estudiar esa posibilidad. Se calculó las raíces del polinomio de Taylor que aproxima a e^z con precisión de mil dígitos significativos, comparando este resultado con los obtenidos previamente con el programa ``cmuller'' los resultados concuerdan. A menos que se requiera una precisión mayor podemos tomar los valores de las raíces como correctos.

Para ilustrar los errores que se generan cuando falla la precisión con el programa Mathematica calculamos la aproximación de la exponencial de grado setenta y cinco ( poly := Normal[ Series[ Exp [z], z, 0, 75 ] ] ) en la forma estándar ( NSolve[poly==0, z] ) y en la forma que se define mayor precisión (NSolve[poly==0, z, 50]) se obtuvieron las siguientes gráficas:

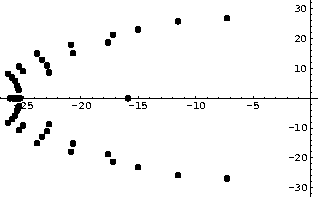
$\begin{figure} \centering \begin{picture} (200,145)(0,0) \put(0,0){\epsfxsize=200pt \epsffile{aepg75e.eps}} \end{picture}\end{figure}$

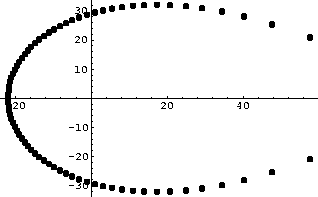
$\begin{figure} \centering \begin{picture} (200,145)(0,0) \put(0,0){\epsfxsize=200pt \epsffile{aepg75.eps}} \end{picture}\end{figure}$

El programa en Mathematica que genera las gráficas previas es:

   RootPlot[poly_, z_] :=
        ListPlot[ {Re[z], Im[z]} /.
                  NSolve[poly==0, z, 50],
                  Prolog -> PointSize[0.02] ] /;
                  PolynomialQ[poly,z]

y se le llama así:

     RootPlot[poly, z]

Para observar cómo se comportaba el polinomio de Taylor que aproxima a la exponencial alrededor de puntos distintos al cero, graficamos con Mathematica los ceros de los polinomios de grado 75 en el punto diez y en el punto veinte. Las gráficas correspondientes son:

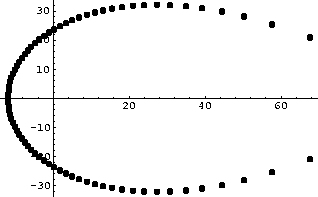
$\begin{figure} \centering \begin{picture} (200,145)(0,0) \put(0,0){\epsfxsize=200pt \epsffile{ae1075.eps}} \end{picture}\end{figure}$

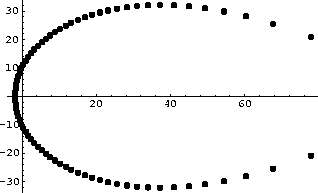
$\begin{figure} \centering \begin{picture} (200,145)(0,0) \put(0,0){\epsfxsize=200pt \epsffile{ae2075.eps}} \end{picture}\end{figure}$

Para ver si había alguna simetría con respecto a la distribución de las raíces graficamos los ceros de los polinomios de Taylor de grado dieciocho y cuarenta y cinco que aproximan a e^-z, la gráficas correspondientes son:

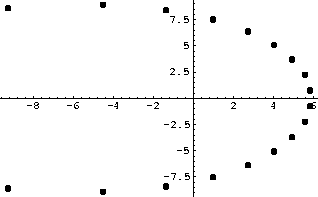
$\begin{figure} \centering \begin{picture} (200,145)(0,0) \put(0,0){\epsfxsize=200pt \epsffile{ameg18.eps}} \end{picture}\end{figure}$

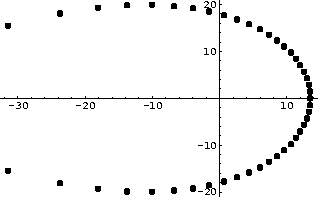
$\begin{figure} \centering \begin{picture} (200,145)(0,0) \put(0,0){\epsfxsize=200pt \epsffile{ameg45.eps}} \end{picture}\end{figure}$

Buscando en la Biblioteca del Departamento, McIntosh encontró otra referencia titulada, ``Zero-Free Parabolic Regions for Sequences of Polynomials" de E. B. Saff y R. S. Varga. En ese artículo se establece la existencia de regiones parabólicas en el plano complejo libres de ceros para algunas secuencias generales de polinomios, y dan como ejemplo de sus resultados que la región:

$\begin{displaymath}y^2 \leq 4(x+1)\ , \ \ \ x> -1 \end{displaymath}$

no tiene ceros para todas las sumas parciales de la función exponencial, dada por la aproximación de Padé. Tomando en consideración lo anterior se generaron dos gráficas, en ambas se muestran las raíces de los polinomios (de grado 1, 5, 10, 15, 20, 25, 20, 35, 40 y 45) de Taylor que ajustan a e^z en el plano complejo junto con la parábola que dan Saff y Varga en un caso, y en el otro se encontró que la región libre de ceros está dada por:

$\begin{displaymath}y^2 \leq 7(x+1)\ , \ \ \ x> -1 \end{displaymath}$

Se determinó este valor tomando como referencia las raíces del polinomio de Taylor de grado sesenta con la parte real más positiva, y como vértice de la parábola -1+0i y el programa ``gep.c''.

Las gráficas mencionadas son:

$\begin{figure} \centering \begin{picture} (260,255)(0,0) \put(0,0){\epsfxsize=260pt \epsffile{aerai1.eps}} \end{picture}\end{figure}$

$\begin{figure} \centering \begin{picture} (260,270) \put(0,0){\epsfxsize=260pt \epsffile{aerai2.eps}} \end{picture}\end{figure}$

Next: Bibliografía Up: Aproximación de e^z a Previous: Planteamiento

Microcomputadoras
2001-02-13