


Next: Raíces
Up: Preliminares
Previous: Preliminares
La primera definición que haremos es la de una función compleja; de
hecho se define de la misma manera que una función real.
Definición 1 (Función Compleja)
Si para cualquier valor de
z en un dominio
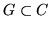
,
le corresponde
un único valor complejo
w, entonces el mapeo
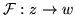
es
una función definida en el dominio
G.
Definición 2 (Límite de una función)
Una función
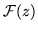
tiene un límite
A cuando
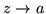
si y solo si se cumple lo siguiente:
Para cualquier
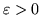
existe un
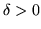
tal que si
entonces
La continuidad en funciones complejas es similar a la continuidad de
las funciones reales:
Definición 3 (Continuidad)
Una función
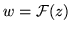
es continua en el punto
z si, para cualquier
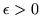
existe un un
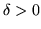
tal que:
Definición 4 (Continuidad Uniforme)
Se dice que una función
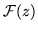
es uniformemente continua en un
conjunto
G si a cualquier
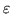
le corresponde un
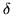
tal
que para dos puntos cualesquiera
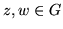
tales que
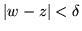
tenemos
Si
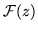 es continua en un conjunto cerrado y acotado entonces es
uniformemente continua.
es continua en un conjunto cerrado y acotado entonces es
uniformemente continua.
Definición 5 (Función Holomorfa)
Si una función es uniforme y continua, y poseé una derivada definida y
continua en cualquier punto, entonces se dice que es holomorfa en el punto.
Definición 6 (Función diferenciable)
Sea la función
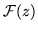
definida en una vecindad del punto
z. Si el
cociente de la diferencia
tiende a un límite finito
A siempre que
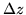
tiende a cero,
entonces el número de
A es llamada la derivada de F en el punto
z y se denota como:
Definición 7 (Función Analítica)
Una función
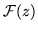
de una variable compleja
z es analítica
en
z=
a si tiene una expansión como serie de potencias
con coeficientes constantes
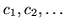
,
que converge absoluta y
uniformemente en algún círculo |
z-
a|<
k, con
k>0.
Otro punto de vista de una función analítica es respecto a la
diferenciabilidad.
Definición 8 (Función Analítica)
Decimos que una función
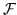
es analítica en una región
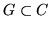
si es diferenciable en cada punto de la región.
De hecho una función
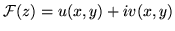 es analítica en un dominio G si las funciones u(x,y) y v(x,y)
son diferenciables en G y cumplen las ecuaciones de direfenciabilidad de
Cauchy-Riemann1.1:
es analítica en un dominio G si las funciones u(x,y) y v(x,y)
son diferenciables en G y cumplen las ecuaciones de direfenciabilidad de
Cauchy-Riemann1.1:
Si
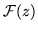 es analítica y diferente de cero en cualquier punto,
en cualquier región, o en el plano completo, así lo es
es analítica y diferente de cero en cualquier punto,
en cualquier región, o en el plano completo, así lo es
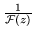 .
.



Next: Raíces
Up: Preliminares
Previous: Preliminares
Microcomputadoras
2001-03-09
![]() es continua en un conjunto cerrado y acotado entonces es
uniformemente continua.
es continua en un conjunto cerrado y acotado entonces es
uniformemente continua.
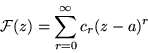
![]() es analítica en un dominio G si las funciones u(x,y) y v(x,y)
son diferenciables en G y cumplen las ecuaciones de direfenciabilidad de
Cauchy-Riemann1.1:
es analítica en un dominio G si las funciones u(x,y) y v(x,y)
son diferenciables en G y cumplen las ecuaciones de direfenciabilidad de
Cauchy-Riemann1.1:
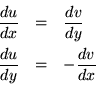
![]() es analítica y diferente de cero en cualquier punto,
en cualquier región, o en el plano completo, así lo es
es analítica y diferente de cero en cualquier punto,
en cualquier región, o en el plano completo, así lo es
![]() .
.