Raíces

Una raíz de una fución compleja ${\cal F}$ es un punto $c \in D$ tal que

$${\cal F} (c) = 0$$ (1.1)

donde D es el dominio de ${\cal F}$.

Si una función ${\cal F} (z)$ es analítica en C, y si el desarrollo de Cauchy-Taylor en c es

$$\sum_{n=k}^{\infty} a_n (z -c)^n$$ (1.2)

con $a_k \neq 0$, entonces se dice que ${\cal F} (z)$ tiene un cero de orden k en c.

Note que la serie inicia en el k-ésimo término, veamos porque los coeficientes $a_1, a_2, \ldots,$ a_k-1 son ceros. Tomemos la expresión 1.2 desde el primer termino:

$$\sum_{n=0}^{\infty} a_n (z - c)^n = a_0 + a_1(z-c)^1 + a_2(... ...+ a_3(z-c)^3 + a_4(z-c)^4 + a_5(z-c)^5 + a_6(z-c)^6 + \cdots$$

Y puesto que si un punto c es un cero de orden k, entonces las derivadas (k-1)-ésimas de la función ${\cal F} (z)$ evaluadas en c son ceros.

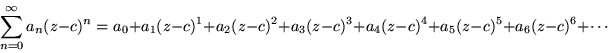
Mostremos de manera explícita la forma de las derivadas, hasta la k-ésima :

$$\begin{eqnarray*}f^{(1)}(z) & = & 1a_1 + 2a_2(z-c)^1 + 3a_3(z-c)^2 + 4a_4(z-c)^3... ...} a_{k+i}(z-c)^i \hspace{1in} \mbox{para $k \geq 1$\space } \\ \end{eqnarray*}$$

Entonces :

$$\begin{eqnarray*}f^{(1)}(c) & = & 0 \\ f^{(2)}(c) & = & 0 \\ f^{(3)}(c) & = & ... ... & \\ f^{(k-1)}(c) & = & 0 \\ f^{(k)}(c) & = & {(k)!}a_{k} \\ \end{eqnarray*}$$

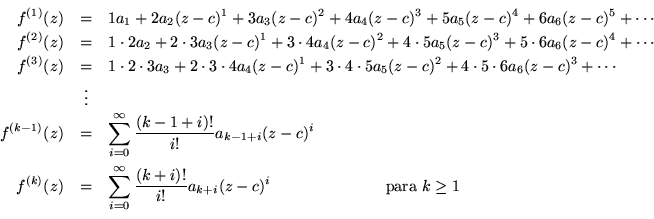
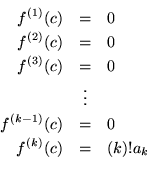
Así tenemos que $a_1, a_2, \ldots, a_{k-1}$ son iguales a cero y $a_k \neq 0$.

Por ejemplo: si c es un cero de orden n=3, tenemos que :

$$\begin{eqnarray*}f^{(1)}(c) & = & 0 \\ f^{(2)}(c) & = & 0 \\ f^{(3)}(z) & = & 1\cdot2\cdot3a_3 \\ \end{eqnarray*}$$

entonces a₁ = 0, a₂ = 0 y $a_3 \neq 0$.

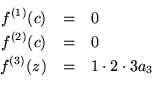
La expresión 1.2 puede factorizarse respecto a el término (z - c) y ésta queda como el producto de dos funciones:

$${\cal F} (z) = g(z) h(z)$$

Con

$$\begin{eqnarray*}g(z) & = & (z - c) \\ h(z) & = & a_k (z-c)^{k-1} + a_{k+1} (z -c)^{k} + \cdots \\ \end{eqnarray*}$$

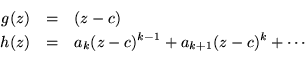
Es decir podemos ``factorizar el cero'' de la función.

En esta sección solo nos resta decir que los ceros de una función no constante son aislados , lo que equivale a decir que si c es un cero, no hay ceros arbitrariamente próximos a c.