



Next: hyperbolic, parabolic, elliptic transformations
Up: Functions of a complex
Previous: Möbius transformations representable as
The fixed points of a Möbius transformation satisfy the requirement
| z |
= |
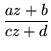 |
(34) |
which translates into the quadratic equation
| cz2 + (d-a) z - b |
= |
0 |
(35) |
with roots
In case c=0 the quadratic term is absent and the single fixed point would be b/(d-a) unless (d-a) were zero. That alternative would leave z without constraint and require b to vanish as well as c. But then all points would be fixed and the transformation would be the identity. And if b did not vanish, the equation would read z=z+b which could not be satisfied unless z were  ,
which might as well be considered admissible.
,
which might as well be considered admissible.
Another case of a single root occurs when the radicand is zero leaving (a-d)/2c as the only fixed point. Otherewise there are always two distinct fixed points




Next: hyperbolic, parabolic, elliptic transformations
Up: Functions of a complex
Previous: Möbius transformations representable as
Microcomputadoras
2001-04-05
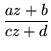
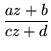
![\begin{displaymath}\frac{1}{c}
\left\{\frac{a-d}{2}\pm\surd
\left[\left(\frac{a+d}{2}\right)^2-1\right]\right\}.\end{displaymath}](img61.gif)