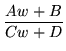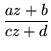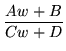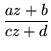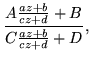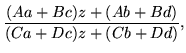Next: eigenvalues and eigenvectors of
Up: Functions of a complex
Previous: Möbius transformations represented as
Although there may be some question of whether the implicit or the explicit form of one-to-one and invertible mappings should be called Möbius transformations, that is the name given to this class of transformations. Mappings often form a group. Since the associative law for their composition is a given, the items to be checked are closure, invertibility and the existence of the identity.
To check closure, consider the composite of two maps. First, suppose we have
| t |
= |
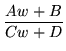 |
(29) |
| w |
= |
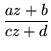 |
(30) |
which gives, on substituting,
| t |
= |
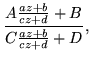 |
(31) |
and, on simplifying,
| t |
= |
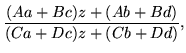 |
(32) |
which mimics the matrix product
From this it is apparent that the 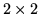 unimodular matrices form a representation of the group of Möbius transformations; in particular the identity is represented by the unit matrix,
unimodular matrices form a representation of the group of Möbius transformations; in particular the identity is represented by the unit matrix,
| z |
= |
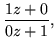 |
(33) |
and the inverse transformation by the inverse matrix.




Next: eigenvalues and eigenvectors of
Up: Functions of a complex
Previous: Möbius transformations represented as
Microcomputadoras
2001-04-05