Eisenstein series

Next, there is a question of what should be averaged, to get a convergent double sum containing the order of n² summands, for a large integer n. Inverse powers of the distance, z^-k come to mind, with k large enough for the size of n^-k to compensate the number of terms yet remaining as one approaches infinity.

An Eisenstein series,

$$\sum_\Omega \frac{1}{(z-z_{ij})^k},$$ S_k(z) = (191)

is an uncomplicated way to get a function for which $S_k(z+m\omega+n\omega') = S_k(z)$. It has poles when $z \varepsilon \Omega$.

When $k \geq 3$ the size of far terms falls off fast enough that there is no problem with the convergence of the double sum, whereas the series for S₁ can reasonably be expected to diverge. The case k=2 sits on the borderline, but the series can be rescued by noticing that the partial sums for one value of z differ by little from those for another value of z.

But it is important to work with the difference of the two series from the outset, and not try to take the difference of their limits. Therefore what might be considered as S₂(Z)-S₂(0) could be written as

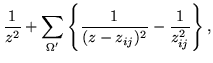$$\wp(x) \frac{1}{z^2} + \sum_{\Omega'} \left\{\frac{1}{(z-z_{ij})^2}-\frac{1}{z_{ij}^2}\right\},$$ = (192)

where the somewhat asymmetrical leading term and the use of $\Omega'$ result from avoiding the formal presence of 1/(0²) in S₂(0).