



Next: restraints on periodic functions
Up: Periodic functions
Previous: Eisenstein series
This function is Weierstrass's 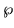 ,
traditionally written with a gothic p, on which he founded the theory of elliptic functions. However,
,
traditionally written with a gothic p, on which he founded the theory of elliptic functions. However,
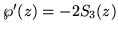 and from there on,
S'k(z) = -kSk+1(z). Looking in the other direction, integrals of
and from there on,
S'k(z) = -kSk+1(z). Looking in the other direction, integrals of  exist, although they are no longer represented by Eisenstein series, and not necessarily periodic nor single valued because of the different paths that could be taken by contour integrals defining them.
exist, although they are no longer represented by Eisenstein series, and not necessarily periodic nor single valued because of the different paths that could be taken by contour integrals defining them.
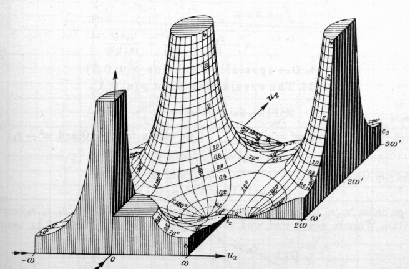
Figure 13:
Jahnke and Emde's drawing of the Weierstrass 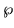 function [16, page 99, figure 55]. The unique double pole is repeated four times because it sits on the corner of a unit cell in the periodic lattice. By uniform multiplicity there are two zeroes, distinct unless forced to coincide by symmetry. Two of the three critical points sit between copies of the double pole, while the third straddles the two zeroes.
function [16, page 99, figure 55]. The unique double pole is repeated four times because it sits on the corner of a unit cell in the periodic lattice. By uniform multiplicity there are two zeroes, distinct unless forced to coincide by symmetry. Two of the three critical points sit between copies of the double pole, while the third straddles the two zeroes.
 |
Nevertheless, there are traditional names and symbols associated with the first two integrals, according to which




Next: restraints on periodic functions
Up: Periodic functions
Previous: Eisenstein series
Microcomputadoras
2001-04-05
![]() ,
traditionally written with a gothic p, on which he founded the theory of elliptic functions. However,
,
traditionally written with a gothic p, on which he founded the theory of elliptic functions. However,
![]() and from there on,
S'k(z) = -kSk+1(z). Looking in the other direction, integrals of
and from there on,
S'k(z) = -kSk+1(z). Looking in the other direction, integrals of ![]() exist, although they are no longer represented by Eisenstein series, and not necessarily periodic nor single valued because of the different paths that could be taken by contour integrals defining them.
exist, although they are no longer represented by Eisenstein series, and not necessarily periodic nor single valued because of the different paths that could be taken by contour integrals defining them.
