 |
= | 0. | (217) |
A differential equation is simply a relationship between a function and its derivatives, usually expressed through the vanishing of such an expression. An equation is considered to be linear if any linear combinations of its solutions is also a solution. The degree of the equation refers to the highest power of a term containing a derivative, whilst its order refers to the highest derivative present.
Thus a second order differential equation contains second derivatives, but there exists a trick whereby it may be replaced by a pair of first order equations. Suppose that the equation reads
 |
= | 0. | (217) |
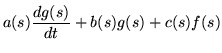 |
= | 0 | (218) |
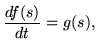 |
(219) |
![$\displaystyle \frac{d}{dt} \left[ \begin{array}{c} g(s) \\ f(s) \end{array}\right]$](img376.gif) |
= | ![$\displaystyle \left[ \begin{array}{cc}
-\frac{b(s)}{a(s)} & -\frac{c(s)}{a(s)} ...
...0 \end{array} \right]
\left[ \begin{array}{c} g(s) \\ f(s) \end{array}\right],$](img377.gif) |
(220) |
Given that higher derivatives may be replaced by a whole series of lower derivatives by using a companion matrix of coefficients, and that the same strategy serves as well for systems of equations, we are free to concentrate our attention on first order linear matrix differential equations. It is moreover desirable to foresee the existence of several solutions according to the selection of an initial vector by subsuming them all into a one matrix rather than several vectors. The linearity of the equation justifies working with square matrices throughout.