There is really no such thing as the derivative of one matrix with respect to another, so the differential calculus of matrices refers to matrices whose elements are functions of a complex variable, and the results of taking derivatives with respect to that variable. It is not unreasonable to work with functions of several complex variables and to take partial derivatives, but the present discussion foresees but one independent variable.
Given a matrix with functional elements, its derivative would be a matrix filled with the derivatives of the individual elements, all in their corresponding locations. Rules for the derivatives of sums, differences, and products are readily obtained from the definitions of the respective operations:
Scalar factors get the same treatment as matrix products, although advantage can be taken of commutativity to simplify results, if necessary. The derivative of a constant matrix is the zero matrix, a result which can be used to calculate the derivative of an inverse matrix. Since
![]() we get
we get
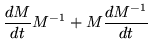 |
= | (221) | |
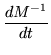 |
= |  |
(222) |
In general, the computation of the derivative of a function defined as an infinite series, or even as a polynomial, will not give the expected result unless the matrix commutes with itself for all values of the parameter, Thus even such a simple result as the derivative of a square becomes
| = | 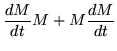 |
(223) |
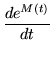 |
= | MeM(t) | (224) |