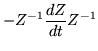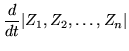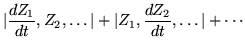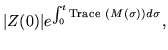linear matrix differential equations

Even agreeing to write differential equations entirely in terms of matrices, without using vectors, there are two different first order equations, depending on whether the coefficient matrix is a left factor or a left factor. Either of the two forms

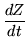$$\frac{dZ}{dt}$$ = M Z (225)

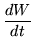$$\frac{dW}{dt}$$ = W M (226)

is possible, not to mention combinations with coefficient matrices on both sides of the unknown matrix and even more complicated combinations. However, the one-sided equations can be interchanged by taking transposes, so it is reasonable to emphasize one of them in preference to the other. Even so, if the coefficient matrix is sufficiently asymmetical, there may be practical advantages to working with the coefficient on one side rather than the other. In any event, we have the rule

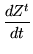$$\frac{dZ^t}{dt} \left\{\frac{dZ}{dt}\right\}^t,$$ = (227)

so

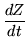$$\frac{dZ}{dt}$$ = M Z (228)

becomes

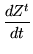$$\frac{dZ^t}{dt}$$ = Z^t M^t. (229)

Another way to put the coefficient matrix on the other side of the variable matrix is to use the inverse matrix. So, if dZ/dt = MZ,

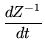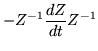$$\frac{dZ^{-1}}{dt} - Z^{-1} \frac{dZ}{dt} Z^{-1}$$ = (230)

= - Z^-1 MZ Z^-1 (231)

= - Z^-1 M. (232)

Note the interesting combination which results from combining the transpose with the inverse, on the one hand, and using an antisymmetric coefficient matrix on the other. That the derivative of the combination Z^-1T is zero makes it constant; once the unit matrix, always the unit matrix, and Z is an orthogonal matrix.

Writing a differential equation for an inverse matrix supposes that there is such a thing, which could be settled by looking at the determinant of the solution. Given that a determinant is made up from products of matrix elements, there should be a formula for the derivative of a determinant as a sum of determinants, in which each column of the original determinant is replaced one at a time by its derivative. But the derivative of the column is just its multiple by the coefficient matrix, so we have

$$\frac{d}{dt}\vert Z_1,Z_2,\ldots,Z_n\vert \vert\frac{dZ_1}{dt},Z_2,\ldots\vert + \vert Z_1,\frac{dZ_2}{dt},\ldots\vert + \cdots$$ = (233)

$$\vert MZ_1,Z_2,\ldots\vert + \vert Z_1,MZ_2,\ldots\vert + \cdots$$ = (234)

$${\rm Trace}\ (M)\ \vert Z_1,Z_2,\ldots,Z_n\vert$$ = (235)

This is an ordinary differential equation with an exponential solution:

$$\vert Z(0)\vert e^{\int_0^t{\rm Trace}\ (M(\sigma))d\sigma},$$ |Z(t)| = 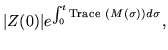(236)

and the characteristic common to exponentials of never vanishing unless it always vanishes. Consequently, the solution matrix of a linear differential equation starting out from a basis of linearly independent initial contions is forever nonsingular.