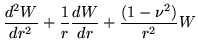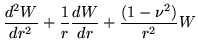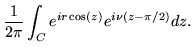Bessel functions

Bessel functions made their first appearance by relating the angular position of a planet moving along a Keplerian ellipse to elapsed time. However the integral and power series shows up in other places, generally concerning the radial variable after separating Laplace's equarion in polar or spherical polar coordinates. However, the radial functions in the Schrödinger equation are Laguerre polynomials, and the one dimensional Schrödinger equation for a constant force are Airy functions which can be transformed into Bessel functions of order 1/3.

Bessel functions obey the differential equation

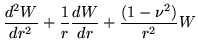$$\frac{d^2W}{dr^2} + \frac{1}{r}\frac{dW}{dr} + \frac{(1-\nu^2)}{r^2}W$$ = 0 (323)

whose distinguishing characteristic is the inverse square singularity at the origin. Consistent with its relationship to polar coordinartes, solutions would be sought in the open interval 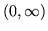$(0, \infty)$, with particular attention being paid to their limiting behaviour at both ends of the interval. That does not mean that efforts have not been made to continue such solutions onto the negative real axis, nor that Bessel functions of imaginary argument are not useful. They bear the same relation to Bessel functions that the hyperbolic cosine bears to the trigonometric cosine.

Consider Sommerfeld's contour integral

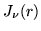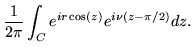$$J_{\nu}(r) \frac{1}{2\pi}\int_Ce^{ir\cos(z)}e^{i\nu(z-\pi/2)}dz.$$ = (324)

which can be verified as solving the Bessel equation. Although it is a question of finding the right exponential, the technique can be applied to a variety of differential equations.

  

Figure 15: Two figures taken from Arnold Sommerfeld's treatise on partial differential equations [26, Figures 18, 19]. He was outstandingly versatile in bringing complex analysis into almost any physical problem.

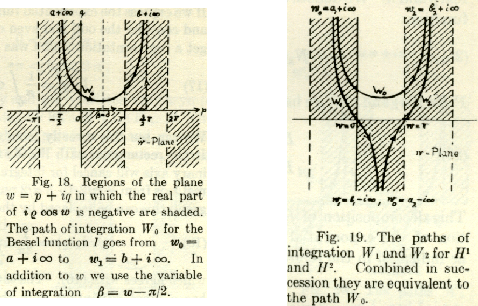Changing the contour of integration gives different varieties of Bessel functions. The common functions resemble sines and cosines. Kelvin's functions are more akin to hyperbolic sines and cosines, for being defined along the imaginary rather than the real axis. Finally, Hankel functions are the analogues of complex exponentials at the unit circle.

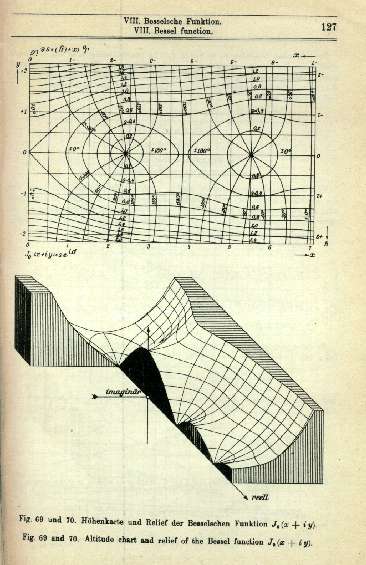
It would hardly be possible not to include a sample of Jahnke and Emde's drawings in a discussion of Bessel Functions, such as the one which can be seen in Figure 16.

  

Figure 16: A perspective view of the modulus of a Bessel function in the complex plane. Typically of such graphs, the function oscillates along the real axis while rising exponentially along the imaginary axis. The figure is a replica of the page containing Jahnke and Emde's drawing of the Bessel function J₀(x+iy) [16, page 127, figures 69 and 70].