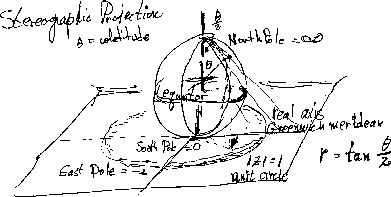
stereographic projection

**Figure 2:** Represention of complex numbers via stereographic projection of a sphere of unit diameter onto a tangent plane.
$\begin{figure} \centering \begin{picture} (300,160) \put(0,0){\epsfxsize=300pt \epsffile{ster.eps}} \end{picture} \end{figure}$

Stereographic projection is often used to reduce the size of the complex plane while preserving some of the characteristics of the plane, such as the angles between intersecting curves. In practice various lines are drawn from a point in such a way that they intersect both a sphere and a plane, although it is easy to imagine two spheres or two planes. The points of intersection common to a given line as it intersects the two surfaces establish the correspondence between the plane and the sphere. In order to use up all the sphere as well as all the plane in the mapping, the plane is usually set up tangent to the sphere, and the source point for the projection is either the opposite pole, resulting in a one-to-one mapping, or else the center of the sphere, by which two diametrically points map to the plane, resulting in a two-to-one mapping.

In the case of the polar stereographic projectionstereographic projection, lines tangent to the pole do not intersect the plane, to which they are parallel. That leaves the pole without an image, but it can be called ``infinity'' and treated as though it were part of the complex plane. In this representation, the unit circle corresponds to the equator of the sphere, whose axis lies perpendicular to the plane. Zero is the point of tangency which could be supposed to be the south pole, infinity is accordingly the north pole, and the real axis might be regarded as the Greenwich meridian. Great circles map into straight lines, other circles into lesser circles.

In this mapping, inversion (mapping z into 1/z) turns the sphere over, allowing infinity to be treated as the reciprocal of zero, and conversely. There is only one infinity; by including it the complex plane can be made compact. Numbers of sufficiently large modulus constitute neighborhoods of infinity, but in working with the sphere rather than the plane, the use of large numbers is avoided.

**Figure 3:** Represention of complex numbers via gnomonic projection of a sphere of unit radius onto a tangent plane.
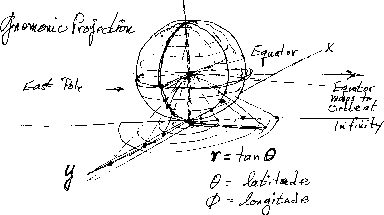$\begin{figure} \centering \begin{picture} (300,140) \put(0,-20){\epsfxsize=300pt \epsffile{gnom.eps}} \end{picture} \end{figure}$

The central, or gnomonic, projectiongnomonic projection maps the equator into infinity, which then consists of a ``line,'' and not a point. Consequently there would be directions at infinity; plus infinity would be distinct from minus infinity, and both from the two purely imaginary infinities. The arrangement can still be compact by taking the sphere with opposite points identified as the representative of the complex plain, but all those different directions still have to be respected.