The stereographic representations of the complex plane are obtained by real constructions. Instead, the complex analogue of the representation of the trigonometric functions could be used, in which the tangent of an angle is the point of intersection of the radius of the unit circle prolonged to intersect the vertical tangent at x=1. The basic representation holds that the x-projection of the radius is
![]() ,
and that the y-projection is
,
and that the y-projection is
![]() .
.
The complex equivalent of this mapping needs a complex angle to work with, and ought to correspond to the polar stereographic projection rather than the central stereographic projection. In the former case, the modulus of the projection is
![]() rather than
rather than
![]() ,
so the suggested mapping is
,
so the suggested mapping is
![]() .
But then,
.
But then,
| = | (14) | ||
| = | 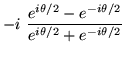 |
(15) | |
| = | 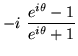 |
(16) | |
| = | (17) |
One great advantage of this representation is that the whole right half-plane, the one whose numbers have positive real parts, is mapped into the unit circle, the imaginary axis taking up residence on its circumference. The real axis maps into the real axis, but given that infinity maps into 1, the whole coordinate grid of lines parallel to the real and to the imaginary axis ends up as as two families of mutually orthogonal circels, all passing through 1.