| = | M(z) Z(z), | (341) |
The form in which the initial value differential equation for a pair of first order equations is written can be called its standard form,
| = | M(z) Z(z), | (341) |
 |
= | (342) |
Here ![]() takes the place of M from the standard equation, but without any eigenvalue which M might have contained. The factor
takes the place of M from the standard equation, but without any eigenvalue which M might have contained. The factor ![]() ,
only half of whose derivative is written explicitly (the other half being combined with M in
,
only half of whose derivative is written explicitly (the other half being combined with M in ![]() ). allows for the possibility of attaching multipliers to the derivatives, which is sometimes either necessary or convenient. Finally,
). allows for the possibility of attaching multipliers to the derivatives, which is sometimes either necessary or convenient. Finally, ![]() positions the eigenvalue where it belongs in the matrix multiplier of Z.
positions the eigenvalue where it belongs in the matrix multiplier of Z.
If ![]() is invertible, it is easy to interconvert the standard and canonical forms; if it is not, the order of the system of differential equations ought to be reduced. By inspection,
is invertible, it is easy to interconvert the standard and canonical forms; if it is not, the order of the system of differential equations ought to be reduced. By inspection,
| M(z) | = |  |
(343) |
There is a further innovation, which consists in introducing the adjoint of the canonical equation,
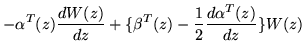 |
= | (344) |
If the combination of signs and transposes seems mystifying, think of the adjoint W as the transpose of the inverse of Z. More exactly, direct substitution and invoking the uniqueness of solutions relative to initial conditions,
| ZA | = | (345) |
| = | (346) | ||
| = | (347) |
There are conditions under which an operator is just the same as its adjoint;
by comparison they are
| = | (348) | ||
| = | (349) | ||
| = | (350) |
Once the definitions have all been established, Green's formula, which asserts that
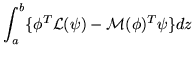 |
= | (351) |
If the vectors ![]() and
and ![]() are eigenvectors,
are eigenvectors,
| = | (352) | ||
| = | (353) |
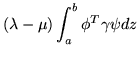 |
= | (354) |
The matrix form of these results is more complicated than the version which is usually seen in textbooks, but it has the advantage of broad applicability. For example, for Schrödinger's equation,
| = | ![$\displaystyle \left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right].$](img598.gif) |
(355) |
The selfadjoint ![]() is antisymmetric - a multiple of
is antisymmetric - a multiple of ![]() - turning the inner product
- turning the inner product
![]() into a determinant; concretely, the Wronskian of the solutions
into a determinant; concretely, the Wronskian of the solutions ![]() and
and ![]() ,
in the case of the Schrödinger equation.
,
in the case of the Schrödinger equation.
The Christoffel-Darboux formula establishes the orthogonality of solutions belonging to different eigenvalues, but cannot establish a norm because of the zero factor resulting from equal eigenvalues. The norm might be gotten as a confluent case, taking limits as two eigenvalues approach, or the undefined norm might just be left in place in expansion formulas.
By using Hermitean conjugates instead of transposes in the relevant formulas, and treating the eigenvalue as a complex variable, the factor turns into
![]() which leaves the imaginary part of the eigenvalue when the two eigenfunctions are the same. The real result can be gotten by taking the limit as the imaginary part vanishes.
which leaves the imaginary part of the eigenvalue when the two eigenfunctions are the same. The real result can be gotten by taking the limit as the imaginary part vanishes.
Supposing that
| f(z) | = | 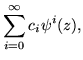 |
(356) |
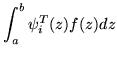 |
= | 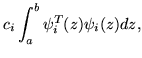 |
(357) |
| ci | = | 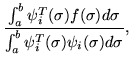 |
(358) |
The Stieltjes integral comes into play when we find that the eigenfunctions are quite numerous and the actual separation between eigenvalues is very small but nevertheless the eigenvalues are packed irregularly. It is also desirable to separate the parts of the coefficient which are due to integrating to function to be represented, and the small factor occasioned by the large norm.
Therefore, keep the integral of the function as a coefficient
| = | 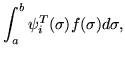 |
(359) |
Altogether,
| f(z) | = | 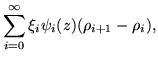 |
(360) |
| = | 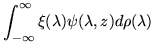 |
(361) |
There still remains the selection of an appropriate right hand boundary condition, and the choice of a uniform normalization for all the eigenfunctions. Help in making the selections can be had from looking at Parseval's equality,
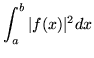 |
= | 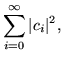 |
(362) |
| (f,f) | = | 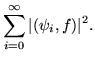 |
(363) |
By the Christoffel-Darboux formula, and using the complex version of Green's formulas rather than the real version,
-[f,f](a)}{\lambda-\lambda^*}$](img616.gif) |
= | ![$\displaystyle \sum_{i=0}^\infty\frac{\vert[f,\psi_i(b)]-[f,\psi_i(a)]\vert^2}
{\vert\lambda - \lambda_i\vert^2}$](img617.gif) |
(364) |
Having turned integrals in function space into boundary sums (an interval has just two boundary points, a and b), it would be convenient to eliminate the dependence on b. One mechanism is to look at a solution
![]() which is a combination of the two standard solutions, and to suppose that f satisfies a real boundary condition at b, resulting in
[f,f](b)=0.
which is a combination of the two standard solutions, and to suppose that f satisfies a real boundary condition at b, resulting in
[f,f](b)=0.
Whatever that boundary condition, it should be used for the ![]() 's as well; in other words,
's as well; in other words,
| = | 0 | (365) |
Having removed the influence of the right boundary point by working with real boundary values in the complex domain, there remains the left boundary to assign some standard form. Using real values there too, and recalling the two linearly independent solutions ![]() and
and ![]() ,
altogether,
,
altogether,
| = | 0 | (366) |
 |
= | 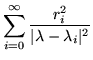 |
(367) |
| = | 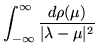 |
(368) | |
| = | 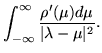 |
(369) |
The description of the spectral density calls for some care in its presentation. In works on solid state theory especially, the spectral density is often considered to be ``the number of eigenvalues per unit of frequency interval,'' which is only a part of the story. This works well for plane waves, or functions which are more or less homogeneous throughout their extent, but a much more important consideration is the relationship between near amplitude and far amplitude. That determines the weight any given function requires to build up a given wave packet, and it is that weight which is properly the spectral density.
A good way to appreciate the difference is to return to the Dirac Harmonic Oscillator previously discussed. The spectrum is continuous, and there is no particular reason to think of the number of eigenvalues per unit interval because they are pretty much uniformly distributed. But most of them dissipate the presence of their particle by their large relative amplitude at infinity. Only eigenvalues in small, selected, intervals contribute to the presence of a particle near at hand, and it is this emphasis which assigns them a high spectral density.
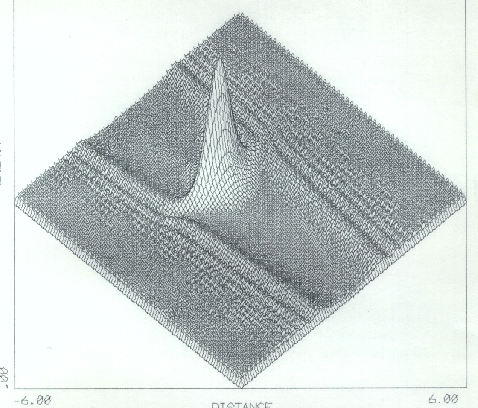 |
Figure 26, although it graphs probability density as a function of both energy and distance, has been normalized to unit amplitude at infinity, so the values over zero distance portray the Titchmarsh-Weyl m-function, or in other words, the spectral density.
Whereas it might be overly ambitious to write
| = |  |
(370) |