graphical representation of complex functions

Although the use of either cartesian or polar coordinates in a plane gives a way to illustrate complex numbers, it is still not so easy to work with all the properties of complex numbers. While complex addition is nothing but vector addition, complex multiplication has two different aspects. A real factor changes scale, just as it does for the real line and for vectors in general. But multiplication by i rotates by $90^\circ$ counterclockwise about the origin, with a further change of scale if i has a multiplier of its own. It is an interesting historical remark, to recall that Hamilton is remembered as having invented quaternions by trying to do the same thing in three dimensions.

Still, thinking of a complex plane brings a certain amount of order to working with complex numbers. But what is to be done with complex functions, even of a single variable? Real tradition graphs the function in the real plane as a cartesian product of the two number sets, the range and the domain, paired by the function. To do the same with complex numbers would require four dimensions - the cartesian product of two planes - which lies beyond anyone's ordinary experience.

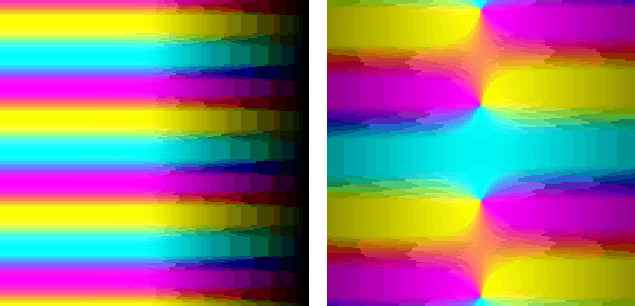
A compromise is to graph part of the function in three dimensions, or in three dimensions as seen in perspective. The usual choice is to graph the absolute value, a positive real number, as a function of the real and imaginary parts of the variable. Variations on this presentation consist of graphing only contours while confining the whole presentation to a plane, or in coloring the three dimensional surface with additional information, such as the phase of the function value.

Figure 1 shows how the function (z-1)/(z⁶-1) may be described in these terms. The absolute value is shown via its traces along lines parallel to the real and imaginary axes, yet colored according to the signs of the real and imaginary parts of its value.

As a further item of interest, there are some patches drawn in red, where the derivative of the function is small. This anticipates a result to be proven later on, that the zeroes of the derivative of an analytic function lie within the convex hull of the function's own zeroes. Looking arounf for saddle points gives an idea of why this theorem should be true.

  

Figure 5: The representation of complex functions by color coded contours. Left: the identity mapping, which shows the natural coloring of the complex plane under this scheme. Notice an ever so slight radial darkening. Middle: the function w=z² showing its values according to the same scheme. The function is lower than its argument within the unit circle, but then it increases rapidly outside, a difference reflected in the brightness of the colors. Right: the function z³ continues the tendency established by the first two powers, of running n times around the color wheel on account of the n^th power, Meanwhile the interior and exterior of the unit circle is more sharply differentiated, but the bottom is flattish even though the function is odd (with respect to negating its argument). Of course, that is a consequence of taking the absolute value which flips everything so that it can always be positive.

When graphs were drawn by hand or with line plotters, it was quite an art to choose appropriate lines, perspectives, and contours to get a good artistic rendition. With color television style monitors, there is a temptation to work more with areas filled with little colored dots, and to forget all the lines. From such a view point, the absolute value of a function could be represented in shades of grey, leaving the color wheel for the phase of the function.

  

Figure 6: The complex exponential (left) rises slowly from zero at the far left to infinity at the far right. The hyperbolic cosine adds this to its rotated (because of the differing signs of the exponents) image.

Although all these color images are very beautiful, they still have to be chosen with care to give them the greatest information content. Using them to make stereopairs is a possibility, although few people seem to be able to visualize raw stereopairs without some form of optical enhancement.

  

Figure 7: A stereopair constructed from slightly shifted renditions of the colorized version of the contours of the square function w = z².