Three dimensional quadratic approximation

The quadratic approximation in three dimensions involves ten basis monomials, and thus an $11 \times 11$ Vandermonde determinant.

$$\left\vert \begin{array}{ccccccccccc} 1 & 1 & 1 & 1 & 1 & 1 ... ... & w_7 & w_8 & w_9 & w_{10} & w \end{array} \right\vert = 0.$$

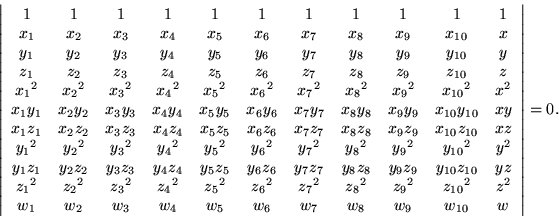
The quadratic form Q now requires a $4 \times 4$ matrix

$$Q=\left[\begin{array}{cccc} J & I & H & G \\ I & F & E & D \\ H & E & C & B \\ G & D & B & A \end{array}\right].$$

If it is given the same treatment as the matrix for two dimensional quadratic approximations, we can make one of its eigenvalues vanish, leaving three others to contend with. There will be many more sign combinations to contend with, but in principle a choice such as

$$(ZU)^T=\left[\begin{array}{cccc}0&\alpha t&\cos\ t&\sin\ t\end{array} \right]$$

will result in a spiral running over the surface of whatever sphere or hyperboloid corresponds to the diagonal form of the matrix, and thus a means of visualizing the contour surface.

Since the coordinate cubes have only eight vertices, two additional data points have to be found to make up the required ten data points. The most symmetric points in the coordinate grid would be a pair of opposite points lying on the extension of one of the body diagonals of the cube.