![\begin{displaymath}D = \left[ \begin{array}{rrr}
0 & 1 & 0 \\
0 & 0 & 1 \\
-c & -b & -a
\end{array} \right], \end{displaymath}](img5.gif)
The Vandermonde matrix and its determinant have such a regular structure that it is worth examining it in further detail. One starting point is the matrix
![\begin{displaymath}D = \left[ \begin{array}{rrr}
0 & 1 & 0 \\
0 & 0 & 1 \\
-c & -b & -a
\end{array} \right], \end{displaymath}](img5.gif)
![\begin{displaymath}\left[ \begin{array}{rrr}
0 & 1 & 0 \\
0 & 0 & 1 \\
-c &...
...]=
\lambda \left[ \begin{array}{c}1\\ u\\ v\end{array}\right]. \end{displaymath}](img6.gif)
Accordingly the components of the eigenvector satisfy
| u | = | (4) | |
| v | = | (5) | |
| -c-bu-av | = | (6) |
| = | (7) |
The advantage of this discovery is that it is equally easy to deduce the row eigenvectors of D, which is a painless way to invert the Vandermonde matrix, due to the biorthogonality of the two sets of eigenvectors..
![\begin{displaymath}\left[ \begin{array}{rrr}u&v&1\end{array} \right]
\left[ \be...
...ght]=
\lambda \left[ \begin{array}{ccc}u&v&1\end{array}\right] \end{displaymath}](img13.gif)
This time the components of the eigenvector satisfy
| -c | = | (8) | |
| u-b | = | (9) | |
| v-a | = | (10) |
Again the eigenvector components are defined by a recursive process which can be followed if the constants are understood to be homogeneous product sums of the eigenvalues. Thus c, which is the product of all the eigenvalues, is divided by one of them (say ![]() )
to obtain u. To obtain v, the product from which
)
to obtain u. To obtain v, the product from which ![]() was just omitted is subtracted from the sum of all products in which one factor at a time is omitted, leaving products from which the factor
was just omitted is subtracted from the sum of all products in which one factor at a time is omitted, leaving products from which the factor ![]() can be divided out. The process continues in similar fashion to produce a vector whose components are the coefficients of the polynomial
can be divided out. The process continues in similar fashion to produce a vector whose components are the coefficients of the polynomial
| = | 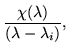 |
(11) | |
| = | (12) |
The inverse of the Vandermonde matrix requires normalized row eigenvectors, obtainable by dividing the i-th row by
![]() ,
which turns out to be
,
which turns out to be
![]() .
The polynomials
.
The polynomials ![]() whose coefficients form the rows of the inverse matrix, are usually written in factored form and are widely known as Lagrange interpolation polynomialsLagrange interpolation polynomials; they are now written as a sum of powers to fit the matrix format. For n+1 data points,
whose coefficients form the rows of the inverse matrix, are usually written in factored form and are widely known as Lagrange interpolation polynomialsLagrange interpolation polynomials; they are now written as a sum of powers to fit the matrix format. For n+1 data points,
| = | 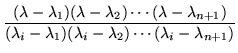 |
(13) | |
| = | (14) |
| M-1 | = | ![$\displaystyle \left[ \begin{array}{ccc}
\pi_{11} & \pi_{12} & \pi_{13} \\
\pi_{21} & \pi_{22} & \pi_{23} \\
\pi_{31} & \pi_{32} & \pi_{33}
\end{array} \right]$](img27.gif) |
(15) |
| = | ![$\displaystyle \left[ \begin{array}{ccc}
\frac{x_2x_3}{(x_1-x_3)(x_2-x_1)} & \fr...
..._1+x_2}{(x_1-x_3)(x_2-x_1)}
& \frac{1}{(x_1-x_3)(x_2-x_1)}
\end{array} \right].$](img28.gif) |
(16) |
Of course, inserting these results into
y=YT M-1 X yields Lagrange's formula,
| y | = | 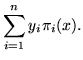 |
(17) |