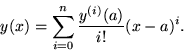


Next: Specialized data points
Up: Contours for <PLOT>
Previous: The Vandermonde matrix
Suppose that in the first example,
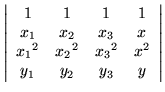 |
= |
0, |
(18) |
x2 = x1, which could happen if the data points were not distinct. By repeating a column, the determinant would vanish, invalidating the ensuing derivation when it came time to divide by the Vandermonde determinant. Foreseeing such a coincidence, the first column could be subtracted from the second without altering the determinant's value. Then,
 |
= |
0. |
(19) |
Recognizing
(y2 - y1)/(x2 - x1) as an approximation to a derivative, the common factor
(x2 - x1) could be removed from the second column and discarded, inasmuch as the vanishing of the surviving determinant will now take place on its own merits.
The result will be
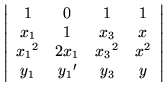 |
= |
0. |
(20) |
Given clusters of data points, it is not hard to see that higher derivatives can be used to remove the redundancies. At one extreme, all the points coincide so all the successive derivatives would be used, resulting in a taylor seriestaylor series.
The result would be
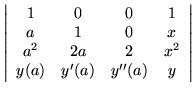 |
= |
0. |
(21) |
which works out to be
| y(x) |
= |
![$\displaystyle \left[ \begin{array}{ccc} y(a) & y'(a) & y''(a) \end{array} \righ...
...array} \right]^{-1}
\left[ \begin{array}{c} 1 \\ x \\ x^2 \end{array} \right]$](img33.gif) |
(22) |
| |
= |
![$\displaystyle \frac{1}{2}
\left[ \begin{array}{ccc} y(a) & y'(a) & y''(a) \end{...
...\end{array} \right]
\left[ \begin{array}{c} 1 \\ x \\ x^2 \end{array} \right]$](img34.gif) |
(23) |
| |
= |
![$\displaystyle \left[ \begin{array}{ccc} y(a) & y'(a) & y''(a) \end{array} \right]
\left[ \begin{array}{c} 1 \\ x-a \\ \frac{1}{2}(x-a)^2 \end{array} \right],$](img35.gif) |
(24) |
generalizing to the well-known formula
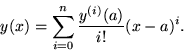 |
(25) |
A more moderate arrangment would coalesce the data in distinct pairs to define polynomials in terms of their values and derivatives at selected points, something known as Hermite interpolationHermite interpolation.



Next: Specialized data points
Up: Contours for <PLOT>
Previous: The Vandermonde matrix
Microcomputadoras
2001-01-15
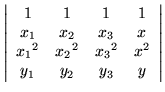
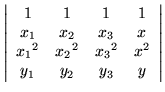

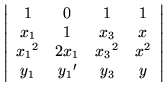
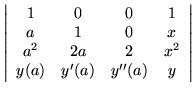
![$\displaystyle \left[ \begin{array}{ccc} y(a) & y'(a) & y''(a) \end{array} \righ...
...array} \right]^{-1}
\left[ \begin{array}{c} 1 \\ x \\ x^2 \end{array} \right]$](img33.gif)
![$\displaystyle \frac{1}{2}
\left[ \begin{array}{ccc} y(a) & y'(a) & y''(a) \end{...
...\end{array} \right]
\left[ \begin{array}{c} 1 \\ x \\ x^2 \end{array} \right]$](img34.gif)
![$\displaystyle \left[ \begin{array}{ccc} y(a) & y'(a) & y''(a) \end{array} \right]
\left[ \begin{array}{c} 1 \\ x-a \\ \frac{1}{2}(x-a)^2 \end{array} \right],$](img35.gif)