Three-point two-dimensional approximation

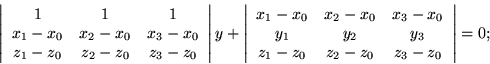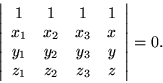
The fundamental hypothesis of the <PLOT> contour programs is that linear interpolation will suffice. Since the monomials 1, x, and y form a basis or first degree functions of two variables, the Vandermonde matrix for the combination will have dimension 3. Usually planar data is taken from a square or rectangular grid; if the corners of the grid squares are used as base points, there will be one too many. Rather than worry about all the ways that contour lines can cross a square, <PLOT> divides each square into two triangles, which are then treated separately. The three vertices of each half square fit nicely into the interpolation formula. When the approximation of linearity is grossly erroneous, the existence of a preferred diagonal becomes quite visible in the erratic wanderings of the contour.

For this case the basic equation has the form

$$\left\vert \begin{array}{cccc} 1 & 1 & 1 & 1 \\ x_1 & x_2 ... ...y_3 & y \\ z_1 & z_2 & z_3 & z \end{array} \right\vert = 0.$$

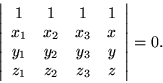
The Vandermonde matrix is

$$M = \left[ \begin{array}{ccc} 1 & 1 & 1 \\ x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \end{array} \right].$$

The inverse matrix is

$$M^{-1} = \frac{1}{V} \left[ \begin{array}{ccc} x_2y_3-y_2x_... ...3 \\ x_1y_2-y_1x_2 & y_2-y_1 & x_2-x_1 \end{array} \right],$$

with Vandermonde determinant

V = x₂y₃+x₃y₁+x₁y₂-y₂x₃-y₃x₁-y₁x₂.

However it is arrived at, the equation can be exhibited in the explicit form

$$\left\vert \begin{array}{ccc} 1 & 1 & 1 \\ y_1 & y_2 & y_... ... y_2 & y_3 \\ z_1 & z_2 & z_3 \end{array} \right\vert = 0.$$

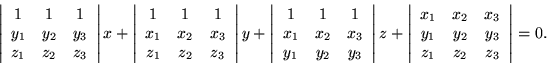
For the purposes of contouring, it is fortunate that the basic equation is an implicit equation of considerable symmetry. For purposes of interpolation, z can be expressed as a function of x and y, but it is equally possible to assign z a value and solve for y as a function of x.

Even so, the equations appear rather formidable. If a specific contour value z₀ has been chosen, the term in z can be combined with the constant term obtain an equation for a line in a plane:

$$\left\vert \begin{array}{ccc} 1 & 1 & 1 \\ y_1 & y_2 & y_... ...\ z_1-z_0 & z_2-z_0 & z_3-z_0 \end{array} \right\vert = 0.$$

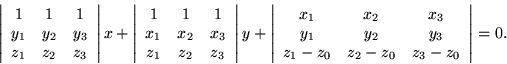
For uniformity of appearance, z₀ could be subtracted from the last rows of the two left hand determinants. Further consolidation results from selecting a specific value for one of the remaining variables, say x₀. Then the formula for y would be

$$\left\vert \begin{array}{ccc} 1 & 1 & 1 \\ x_1-x_0 & x_2-... ...\ z_1-z_0 & z_2-z_0 & z_3-z_0 \end{array} \right\vert = 0;$$

still, this and similar results follow directly from original determinant.