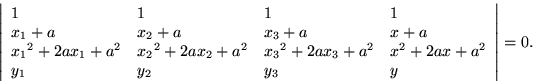
It would appear to be necessary to invert the Vandermonde matrix for each grid square; however, the use of a uniform grid results in so much symmetry that the same Vandermonde matrix can be used throughout the grid. The reason can be seen by returning to the Vandermonde matrix for quadratic interpolation, with a translated origin:
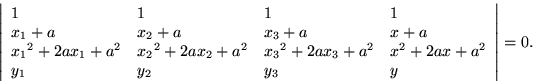
By straightforward determinantal algebra it can be seen that this determinant is the same as the untranslated determinant, but factoring the determinant is more informative.
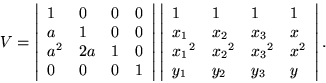
The determinant on the left, having the value 1, is nonsingular; translation preserves the validity of the interpolation equation even as it rearranges its coefficients. Other changes of basis should be handled the same way, by factoring out the responsible matrix. Nor are admissible changes confined solely to the independent variables; for example the zero point for the the dependent variable could be changed. Not often do we find transformations which mix the dependent variable with the independent variables, although they are just as admissible as any others within the framework of the theory.
Although it is not performed as frequently, changing scale follows the same process as translating the origin. We need the matrix

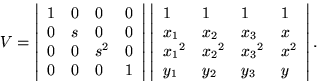
As a general proposition the expansion of a polynomial according to a prescribed basis with determined coefficients can be considered to be the inner product of two vectors. The row, say, carries the coefficients as coordinates while the column is outfitted with the members of the basis. Accordingly, whenever a change of basis is made, such as referring the set of points to a new origin, the inverse matrix of the change can be applied to the coefficients to get a new expansion formula.
The case of translation, which we are examining, has an inverse matrix of typical form
| T-1 | = | ![$\displaystyle \left[ \begin{array}{cccc}
1 & 0 & 0 & 0 \\
-a & 1 & 0 & 0 \\
a^2 & -2a & 1 & 0 \\
-a^3 & 3a^2 & -3a & 1
\end{array} \right],$](img86.gif) |
(48) |
Starting from Maclaurin's series
| p(x) | = | 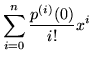 |
(49) |
| p(x) | = | 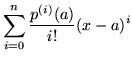 |
(50) |
![$\displaystyle \left[ \begin{array}{c} 1 \\ x-a \\ (x-a)^2 \\ (x-a)^3 \end{array} \right]$](img89.gif) |
= | ![$\displaystyle \left[ \begin{array}{cccc}
1 & 0 & 0 & 0 \\
-a & 1 & 0 & 0 \\
a...
...ay} \right]
\left[ \begin{array}{c} 1 \\ x \\ x^2 \\ x^3 \end{array} \right]$](img90.gif) |
(51) |
![$\displaystyle \left[ \begin{array}{c} p(a) \\ p'(a) \\ \frac{1}{2} p''(a)
\\ \frac{1}{6} p'''(a) \end{array} \right]$](img91.gif) |
= | ![$\displaystyle \left[ \begin{array}{cccc}
1 & a & a^2 & a^3 \\
0 & 1 & 2a & 3a^...
...0) \\ p'(0) \\ \frac{1}{2} p''(0)
\\ \frac{1}{6} p'''(0) \end{array} \right]$](img92.gif) |
(52) |