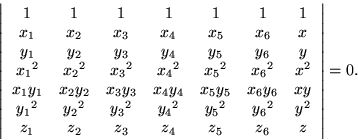
Failure of a linear approximation to a surface will occur whenever the triangulation of the coordinate grid is insufficiently fine, which is normally compensated by reducing the grid size. Near critical points, however, a smaller grid only makes matters worse. The remedy is to use a quadratic approximation, unless the critical point is of still higher order. The most general second degree polynomial in two variables has the form
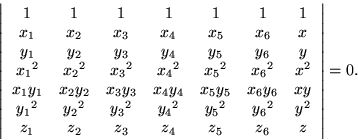
It would not seem to be advisable to try to express such large
Vandermonde determinants in symbolic form, so any particular instance
should be inverted numerically to obtain the row of coefficients
YTM-1. An inhomogeneous second order polynomial can be written as
a quadratic form,
![\begin{displaymath}Q=\left[ \begin{array}{ccc} F&E&D\\ E&C&B\\ D&B&A \end{array} \right].\end{displaymath}](img63.gif)
The contour lines for z can be represented by y as a function of x
if the terms in y are gathered together and expressed as a quadratic
form. Write the previous equation in the form
Nevertheless there is a better way to procede. Traditionally the cross
term is eliminated by rotating x and y,
| x | = | (42) | |
| y | = | (43) |
With further trigonometric manipulation,
 |
(44) | ||
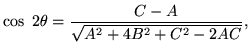 |
(45) |
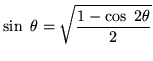 |
(46) | ||
 |
(47) |
Q has not been diagonalized because diagonalization is a transformation of the type Z-1QZ rather than ZTQZ; but the translation which completes the square is not unitary, as would be necessary for the two transformations to coincide.
The two remaining diagonal elements of ![]() may have the same sign, or opposite signs, according to whether the critical point is extremal or a saddle point. Accordingly coefficients of their eigenvectors could be chosen according to one of the following two forms,
may have the same sign, or opposite signs, according to whether the critical point is extremal or a saddle point. Accordingly coefficients of their eigenvectors could be chosen according to one of the following two forms,
It still remains to ascertain how much of the conic section lies within the simplex that will be contoured; one way to avoid the problem would be to graph it through some parameter range, with a visibility function to determine whether the segments to be graphed lie within the chosen simplex or not.
Another important point concerns the location of the six data points needed for quadratic interpolation; one way to obtain them is to choose two consecutive squares from the coordinate grid, and another would be to calculate supplemental points within the square iteslf. Yet another solution would be to work with a triangular or hexagonal grid. Such alternatives tend to be incompatible with normal data acquisition techniques, but might be feasible whenever data could be generated on demand at specified coordinates.