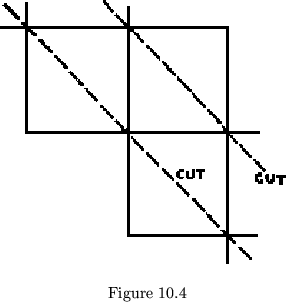
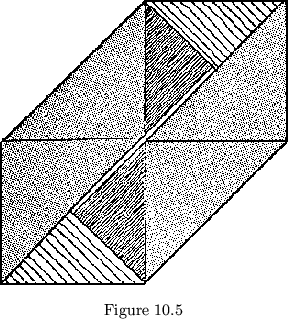
Heretofore it has been assumed that leaves must be congruent, with alternate leaves mirror images of the others. In breaking this convention, we can at the same time begin to show the weakening of class distinction. Consider, for example, the regular(_leafed) proper tetraflexagon of order four. In this flexagon, two adjacent edges of every leaf are occupied by hinges; the others have no function other than maintaining order in the pat. Suppose, then that we chop off the unused corner of each leaf (see fig. 10.4). It is interesting to note that this leaves the plan in the shape of a straight strip of paper, folded off in right isosceles triangles. The flexagon still holds together, it is still of order 4 and cycle 4 (4 hinge positions), but it is now of class 3. Yet, when the flexagon is folded up, it does not at all assume the characteristic shape of a class 3 flexagon: three colors are exposed on each side of each face, and some of the leaves do not meet at the center (fig. 10.5). Is it right, then, for us to be calling this a class 3 flexagon? We will have to reexamine the definition of ``class''. The ``class'' is the number of sides of the component leaf polygons. This flexagon indicates that something more is needed. ``Class'' must also indicate the relative orientation of the leaves. For convenience then, we state that the ``class'' of a flexagon must give an indication, when called for, of this orientation.

It seems clear that we could, in a way analogous to that just shown,
chop off any combination of unhinged edges in any flexagon ![]() . Hence,
the class of a complete or incomplete flexagon of cycle
. Hence,
the class of a complete or incomplete flexagon of cycle ![]() cannot be
established without further information. Also, just as edges can be removed,
they can be added, or the leaves may be perforated or curved leaves
may be used. Anything is allowed, so long as on the one hand it does not
decrease the size of the leaf to the point where it allows the flexagon to
collapse or, on the other hand, it does not increase the leaf in size
sufficiently to interfere with the hinging of other leaves. In performing
these other alterations, the ``class'' motion is completely demolished, so
that ``class'' now becomes a description of the general appearance of each
leaf. Thus the class comes to be identified more and more with the plan,
except that it does not include the sign or number sequences. In fact, the
plan is the sum of these three: class, number sequence, and sign sequences.
cannot be
established without further information. Also, just as edges can be removed,
they can be added, or the leaves may be perforated or curved leaves
may be used. Anything is allowed, so long as on the one hand it does not
decrease the size of the leaf to the point where it allows the flexagon to
collapse or, on the other hand, it does not increase the leaf in size
sufficiently to interfere with the hinging of other leaves. In performing
these other alterations, the ``class'' motion is completely demolished, so
that ``class'' now becomes a description of the general appearance of each
leaf. Thus the class comes to be identified more and more with the plan,
except that it does not include the sign or number sequences. In fact, the
plan is the sum of these three: class, number sequence, and sign sequences.