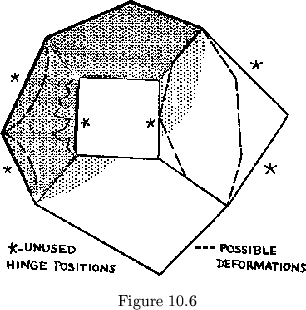
Another descriptive quantity closely associated with the class is the degree of each face. This is defined as the number of hinge positions between the two hinges to each pat, measured about the center of the flexagon, plus one. So long as every hinge position in each pat remains occupied, the face degree is easily determined. However, once we are allowed to mutilate the leaves indiscriminately, by making them from irregular noncoincident leaves, strange things begin to happen. First, if all the hinge positions are occupied, making the leaves irregular will have no effect on the face degree. However, at tubulations on the outer edge of the flexagon's map, for example, as seen in incomplete flexagons, there will always be at least one pat in which not all the hinge positions are taken. Then, if non-coincident leaves are allowed, the number of hinge positions between the incoming and outgoing hinges may be altered by simply chopping some off or adding in some new ones, as in fig. 10.6.

As we shall see in the section on heterocyclic flexagons, these additional
(or fewer) hinge positions may actually be used, along with
more non-coincident leaves, to change the cycle of the flexagon. What
has this done to the face degree? It has not changed the angle between
the hinges to the incoming and outgoing pats, but the degree of only
one pat in each unit has been altered. In fact, it may not be clear
just how many hinge positions there are between incoming and outgoing
hinges. In view of this fact, it would seem sensible to redefine the
face degree as the angle formed by the perpendiculars to the incoming
and outgoing hinges, as shown in fig. 10.7, since this value remains
constant when the number of hinge positions does not. Yet we shall
see that here is the basis for yet another later section, for in compound
faces the face degree actually does assume 2 values for each
unit. Thus the face degree, like the class, becomes purely descriptive
in nature. It, together with the number of units, tells how the
pats will meet at the flexagon's center (if at all). Henceforth, when
the face degree is not referred to in degrees, it must be understood
that it refers to a flexagon of some given cycle with a given shape
of leaf (usually a regular polygon of ![]() edges). This definition is
also superior to the older one in that it clears up the difficulties
that would have arisen in determining the difference between, say a
edges). This definition is
also superior to the older one in that it clears up the difficulties
that would have arisen in determining the difference between, say a
![]() face in a hexaflexagon and a
face in a hexaflexagon and a ![]() face in a triflexagon whose center
had been cut out to facilitate flexing 10.1.
face in a triflexagon whose center
had been cut out to facilitate flexing 10.1.
