Now that ``class'' has dissolved out from under us, the sign sequence can no longer be a simple string of signed numbers; we must now indicate the central angle between the hinges of each leaf. How this is done is irrelevant; the point is that this is the new meaning we must assign each of the terms in the sequence. The real problem, however, arises when we try to use the sign sequence.
Until now, we have adhered to a basic rule of flexagon building which
states that the sum, ![]() , of the terms in the sign sequence must be evenly
divisible by the class; or if we choose to speak in terms of symbols, that
, of the terms in the sign sequence must be evenly
divisible by the class; or if we choose to speak in terms of symbols, that
![]() .
The physical interpretation of this rule is
that, when a unit is folded up with one leaf upon the other, the hinges
entering and leaving this unit pat will coincide.
.
The physical interpretation of this rule is
that, when a unit is folded up with one leaf upon the other, the hinges
entering and leaving this unit pat will coincide.
It is not difficult to see why this rule has always held, heretofore.
All previous flexagons were produced by the slitting process, or, in the
sign sequence, by replacing a given sign with a group of ![]() opposite
signs (for
opposite
signs (for ![]() , incomplete cycles may be viewed in this case as
deletions of complete cycles. Since deletion clearly does not
change the sign sequence sum, incomplete cycles pose no difficulty.)
Hence
, incomplete cycles may be viewed in this case as
deletions of complete cycles. Since deletion clearly does not
change the sign sequence sum, incomplete cycles pose no difficulty.)
Hence ![]() remained constant for a given
remained constant for a given ![]() . Considering only the
one-cycle flexagon of cycle
. Considering only the
one-cycle flexagon of cycle ![]() , therefore, we see that its sign
sequence is composed of
, therefore, we see that its sign
sequence is composed of ![]() like signs, so that
like signs, so that
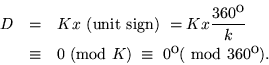
However, in the heterocyclic flexagons made from regular polygonal
leaves, slitting did not replace a sign by ![]() opposite signs;
slitting replaced one sign in the old cycle, where
opposite signs;
slitting replaced one sign in the old cycle, where ![]() , say, by
, say, by
![]() opposite signs, where
opposite signs, where
![]() .
Hence, the sign sequence sums for this slitting are unequal:
.
Hence, the sign sequence sums for this slitting are unequal:
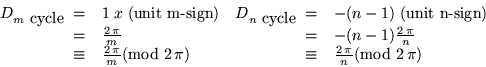
At this point we will either force the difference
![]() to become congruent to zero, by adding in other cycles or by using
one of the techniques for destroying class distinctions given previously,
or we will leave
to become congruent to zero, by adding in other cycles or by using
one of the techniques for destroying class distinctions given previously,
or we will leave
![]() .
.
In the latter case, when the flexagon unit is folded together
into a unit pat, as it is, for example, in flexing, the incoming
and outgoing hinges will not coincide, and the ability to flex will
depend only on the magnitude of ![]() and the elasticity of the materials.
Of course, if we wish to abandon class altogether, the sign sequence
may be juggled around at will, and we need only make the angles have
any values that will satisfy the rule. If we wish to use regular
polygons as leaves,
and the elasticity of the materials.
Of course, if we wish to abandon class altogether, the sign sequence
may be juggled around at will, and we need only make the angles have
any values that will satisfy the rule. If we wish to use regular
polygons as leaves, ![]() , the sum of all discrepancies such as
, the sum of all discrepancies such as
![]() ,
must be computed. In doing this, the terms representing a given
cycle must always be given the same sign in the difference (whenever
,
must be computed. In doing this, the terms representing a given
cycle must always be given the same sign in the difference (whenever
![]() occurs it will always be preceded by a minus sign;
occurs it will always be preceded by a minus sign;
![]() , never).
When
, never).
When
![]() ,
the flexagon will operate without difficulty
(except, of course, the difficulty encountered in overlapping assorted
polygons). It is interesting to note that, as predicted,
,
the flexagon will operate without difficulty
(except, of course, the difficulty encountered in overlapping assorted
polygons). It is interesting to note that, as predicted, ![]() for the
flexagon shown in fig. 12.7
is uninfluenced by the presence of the triangular cycle, but is also
uninfluenced by the pentagonal cycles. The computation for this
flexagon goes:
for the
flexagon shown in fig. 12.7
is uninfluenced by the presence of the triangular cycle, but is also
uninfluenced by the pentagonal cycles. The computation for this
flexagon goes:

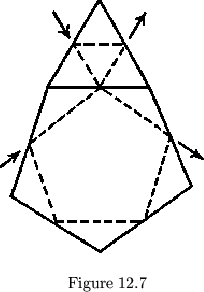
Using this method, the feasibility of a given flexagon may
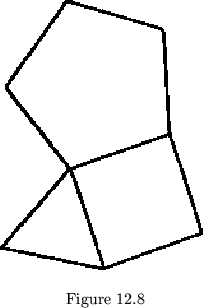
be guessed almost at once. Thus ![]() , for the flexagon shown in fig.
12.8, is clearly quite near to zero, since the difference between
one-fourth, and one-fifth is almost the same as that between one-third
and one-fourth. Or, actually doing the computation,
, for the flexagon shown in fig.
12.8, is clearly quite near to zero, since the difference between
one-fourth, and one-fifth is almost the same as that between one-third
and one-fourth. Or, actually doing the computation,
![]() , and
, and
![]() ,
which is close enough to allow flexing
with reasonably elastic materials.
,
which is close enough to allow flexing
with reasonably elastic materials.
A graphic demonstration of these angle differences is given when the hinge network is constructed. Where two polygons of different types meet, the network lines must be bent (See fig. 12.7).