Heterocyclic flexagons are defined as those made up of two or more
unequal cycles. Thus we have been dealing with heterocyclic flexagons for
a long while, since all incomplete flexagons are heterocyclic. In fact,
the only distinction between incomplete flexagons and other heterocyclic
flexagons is the class, which as we have just seen, is a weak one indeed.
However, the heterocyclic flexagons do present a number of interesting
problems, e.g., their construction, for which reason they are examined
separately.
In introducing the heteroflexagons, we will momentarily not require class uniformity within the flexagon and assume that, rather than working with polygons all of the class of the highest cycle, we are working with regular polygons of the classes equal to the particular cycles in which they are employed. To strengthen the new approach we will start from the beginning and attack the problem with the technical knowledge that we now have available.
We have seen how the addition of a second cycle to a one-cycle
![]() -flexa-gon can be accomplished in steps by the addition of one new side
at a time. It seems clear, then, that the number of sides to be added
in to complete the cycle depends only on the shape of the polygons used.
It is found, naturally enough, that by changing the type of polygon used,
when building the second cycle, we can make this cycle take on any desired
size. For example, by using pentagons, in the proper places, we can add
a pentagonal cycle to a tetraflexagon. A flexagon can then be built
of any combination of cycles, using various plan polygons. Such flexagons
are called heterocyclic flexagons.
-flexa-gon can be accomplished in steps by the addition of one new side
at a time. It seems clear, then, that the number of sides to be added
in to complete the cycle depends only on the shape of the polygons used.
It is found, naturally enough, that by changing the type of polygon used,
when building the second cycle, we can make this cycle take on any desired
size. For example, by using pentagons, in the proper places, we can add
a pentagonal cycle to a tetraflexagon. A flexagon can then be built
of any combination of cycles, using various plan polygons. Such flexagons
are called heterocyclic flexagons.
The justification for suddenly changing the type of leaf may be more
easily seen in another example. Consider a proper flexagon of cycle ![]() in
which one cycle is complete, and a second cycle is one side short of
completion. This means that one more leaf is to be slit, at the empty
hinge position. Suppose, however, that we use only half of this hinge
position, saving the rest by adding in a new edge to our
in
which one cycle is complete, and a second cycle is one side short of
completion. This means that one more leaf is to be slit, at the empty
hinge position. Suppose, however, that we use only half of this hinge
position, saving the rest by adding in a new edge to our ![]() -gons at this
point. The flexagon will clearly operate as effectively as if the leaves
had remained unchanged, for we have done no more than change the angle
between hinges and cut off a corner. However, we do now have another
hinging position, so that we have changed the value of
-gons at this
point. The flexagon will clearly operate as effectively as if the leaves
had remained unchanged, for we have done no more than change the angle
between hinges and cut off a corner. However, we do now have another
hinging position, so that we have changed the value of ![]() . Yet we need not
disturb the completed cycle at all, since it occupies a distinct and
relatively independent position in the pat structure. We thus obtain a
flexagon with cycles of both
. Yet we need not
disturb the completed cycle at all, since it occupies a distinct and
relatively independent position in the pat structure. We thus obtain a
flexagon with cycles of both ![]() and
and ![]() . This method can clearly be
extended to produce any combination of cycles.
. This method can clearly be
extended to produce any combination of cycles.
Heterocyclic flexagons will, of course, have maps made up of mixed polygons.
This does not, however, impair the power of the map of predicting pat
structure and plan shape. The only alteration is that we must
carefully record the signs in terms not only of multiples of a basic pat
rotation unit but in terns of ![]() itself, since
itself, since ![]() assumes varied values.
That is, aside from recording the usual ``+1'' or ``
assumes varied values.
That is, aside from recording the usual ``+1'' or ``![]() '', we must indicate
the type of polygon to which this rotation value corresponds. All of this
information is given in the map: the sign in the usual manner and the
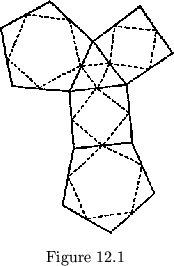
polygon by the polygon in which each hinge network vertex lies (see fig. 12.1).
It is interesting to note that there can be no confusion at the junction of
two cycles, since no sign or number is associated with such a position in
the map. Furthermore, we can have a heterocyclic flexagon in which one
cycle is completely surrounded by different cycles, so that there are no
leaves in the plan having its shape. Such a cycle is the triangle in the
map shown in fig. 12.1. Clearly, the plan for this map is made up entirely
of squares and pentagons.
'', we must indicate
the type of polygon to which this rotation value corresponds. All of this
information is given in the map: the sign in the usual manner and the
polygon by the polygon in which each hinge network vertex lies (see fig. 12.1).
It is interesting to note that there can be no confusion at the junction of
two cycles, since no sign or number is associated with such a position in
the map. Furthermore, we can have a heterocyclic flexagon in which one
cycle is completely surrounded by different cycles, so that there are no
leaves in the plan having its shape. Such a cycle is the triangle in the
map shown in fig. 12.1. Clearly, the plan for this map is made up entirely
of squares and pentagons.
So far, the heterocyclic flexagon seems to be quite adequately treated with no major extension of flexagon theory. However, there are two aspects of these flexagons that have been momentarily overlooked. Each of these is so important to later concepts that it requires special treatment.