C. Pat Structure System.

$$\begin{array}{lllllllll} \;\; & P_h\{k_0\} & , & P_j\{m_k\} &... ...\{m_0\} & , & P_i^*\{n_m\} &\; & \qquad \;\;& (F) \end{array}$$

To use these directions for right-handed flexes in backwards numbered flexagons, let the pats referred to be interchanged, or interchange the pats shown without changing them.

The operation given above as ``flexing'' (F) cannot be repeated upon a flexagon without the use of a new thumbhole, from a second cycle. Thus it should be distinguished from a flex followed by a rotation, which is the operation that is used traveling about a single cycle. This relationship may lead us to look for other properties of the operations that have been established. For this purpose, let us establish the following notation: $XY$ signifies that an operation $X$ is to be performed, to be followed by an operation $Y$. Flex-rotation is $FR$. If $I$ is the identity, then $RR=R^2=I=T^2$. This ``multiplication'' is not necessarily commutative: $FR\neq RF$, but $TR=RT$. We can see the symmetry of the flexing operation if we observe that $(FRT)^2 = I$. If we flex-rotate, the resulting structure can invariably be made to flex again, since it can again be plugged into the flexing expression. Thus it can be proved that if a flexagon can once be flexed it can be flexed in at least 3 distinct situations, in such a way that $(FR)^3=I$. We could define the cycle, $G$, of a given sequence of flexes, by $(FR)^G=I$, where it is understood that the group of leaves represented by $P\{n_x\}$, any $x$, in the instructions for flexing, must contain no thumbholes.

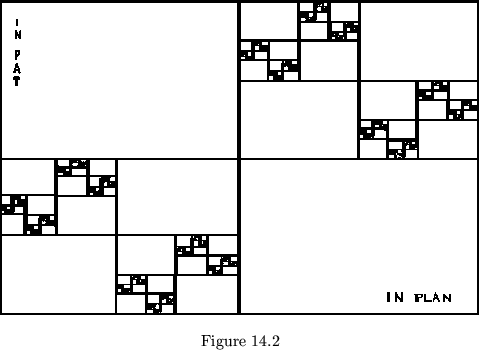
The operations which we have described provide means for a fairly complete discussion of flexagons using paper and pencil only. We can build flexagons up, using sequence of numbers: a flexagon is an ordered pair of pats. A pat is a set of smaller pats, each taken in inverse order, as demonstrated by the diagrams in figures 14.2 and 14.3. We can take any flexagon we build and, by plugging it into one of the operational descriptions we have given, put it through its paces. These arrangements of numbers and the various operations that can be performed upon them may even prove interesting for their own sake.

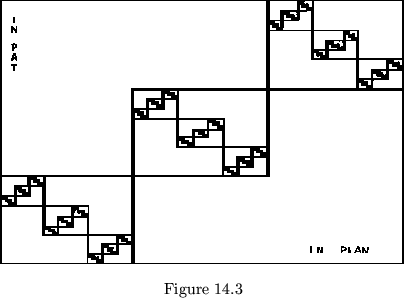
The operations of flexing and rotating may be used to create yet another representation of the flexagon. To reach a given face of a flexagon from some starting point, there is a unique shortest sequence of 0-cut flexes and rotations. No matter what path is used, the faces taken by this shortest route must be included in the route. Hence, using the identities $R^2=I$ and $(FR)^G=I$, any path between the two faces may be reduced to the unique shortest path. The process is shown in fig. 14.4.

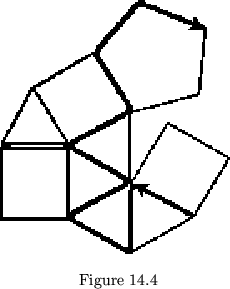
This is because at a given face a rotation will either lead away from the desired face or toward it. If it leads away, backtracking will be necessary. Using this fact, we could let a sequence of flexes and rotations represent each face. In fact, this principle is the basis for the map, as we have seen in the discussion of the covering space (see section 3). Notice, however, that in the pat structure system, faces are not necessarily distinct. Symmetrical spots on the map will be indistinguishable, so that the flex-rotation method of face representation will fail to create the equivalence classes that actually exist in this system.

Now that we can deal effectively with flexagons made up of sequences of numbers, let us return to the cards themselves. Flexing a card flexagon, it will be found, is a real job. Finding which thumbholes are available is the chief problem; the actual flexing is really not too difficult. In fact, all it requires is the putting together of the two pats and their disunion at the chosen thumbhole. Actually, this is all the information that is imparted by the number manipulating operations in the three systems we have discussed. To assist in finding the thumbholes, we may resort to using a map (as is necessary in the number sequence system). On the other hand, a slightly more subtle method is the coloring of the numbered cards according to a system which will embody the map. This is the same as using both number sequence and constant order, and permits us to shuffle the cards and then replace them in order very easily.

Using both number sequence and constant order may lead to the discovery that certain flexagons are dual with other flexagons, or with themselves; that is, the constant order of one is identical with the number sequence of the other, and vice versa. Of course, the sequences may differ (each term of one from the corresponding term of the other) by a constant, but this means that they are identical, and may be detected by comparing the differences of adjacent terms in each of the two sequences, as in section 4.